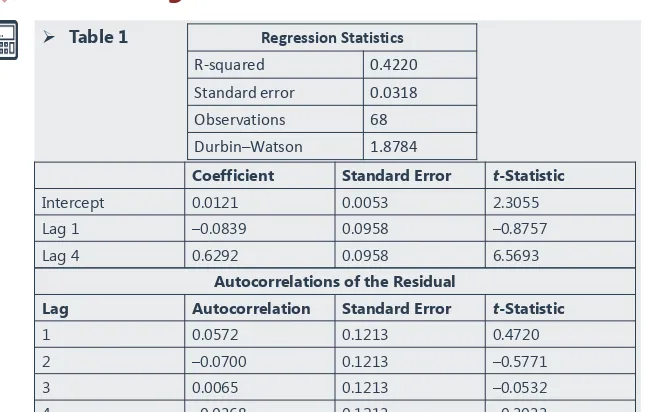
CFA 2018 Level 2 Quantitative methods
Teks penuh
Gambar
Garis besar
Dokumen terkait
[r]
ASEAN Power Grid merupakan proyek kerja sama interkoneksi listrik regional, yang diharapkan dapat menjawab tantangan kebutuhan listrik ASEAN yang terus meningkat. Indonesia,
Keengganan manusia menghambakan diri kepada Allah sebagai pencipta akan menghilangkan rasa syukur atas anugerah yang diberikan sang pencipta berupa potensi yang sempurna yang
Kelompok Muktazilah mengajukan konsep-konsep yang bertentangan dengan konsep yang diajukan golongan Murjiah (aliran teologi yang diakui oleh penguasa
Penentuan sifat biolistrik Kapasitansi (C), Impedansi (Z), dan Konstanta Dielektrik (K) yang berpengaruh nyata terhadap rendemen menggunakan analisis regresi linier
Program Swish 2.0 telah menyediakan beberapa contoh animasi yang dapat anda gunakan untuk membuat animasi baik teks, gambar, button (tombol), link ke halaman lain maupun link ke
masyarakat Melayu Patani di Selatan Thai untuk berunding dengan pihak. kerajaan pusat di
[r]