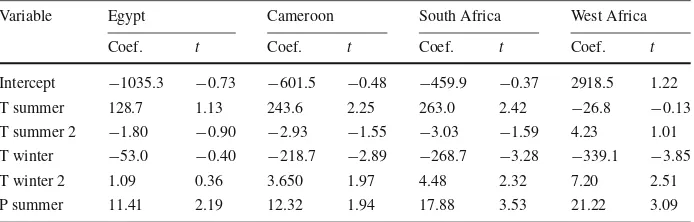
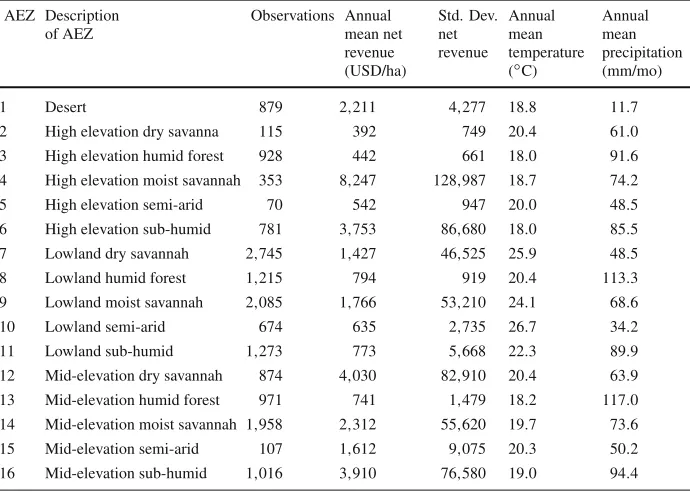
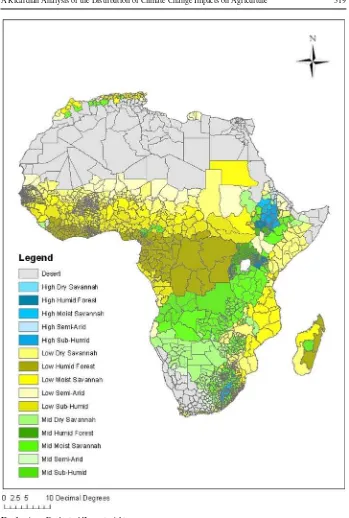
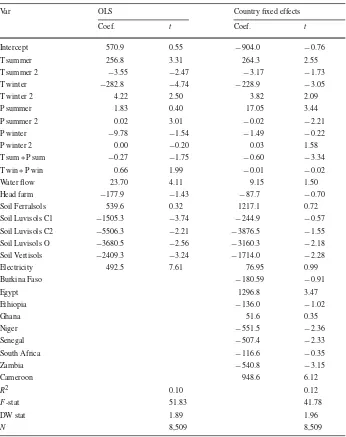
A Ricardian Analysis of the Distribution of Climate Change Impacts on Agriculture across Agro-Ecological Zones in Africa
Teks penuh
Gambar
Dokumen terkait
Sesudah penerapan fasilitas kerja yang ergonomis, terjadi perbaikan sikap kerja pada kelompok perlakuan dan terdapat pengaruh sikap kerja terhadap keluhan muskuloskeletal
Merujuk pada rumusan masalah diatas, tujuan yang ingin dicapai dalam penelitian ini adalah untuk mengetahui persepsi siswa kelas XI terhadap layanan bimbingan klasikal di SMA Negeri
Landasan psikologi dalam pengembangan kurikulum, tiada lain agar upaya pendidikan yang dilakukan dapat menyesuaikan dengan hakikat peserta didik, baik penyesuaian dari segi materi
Dengan maksud hasil penelitian ini untuk meneliti tentang proses pembelajaran seni budaya khususnya pada pembelajaran suling Sunda lubang enam, dimana siswa memiliki
Dan m asih banyak lagi shalaw at yang dit unt unkan oleh Nabi Shallallahu 'alaihi w assallam. Adapun shalaw at - shalaw at yang m enyelisihi t unt unan Nabi Shallallahu
Dihisab oleh: Oman Fathurohman SW - Majelis Tarjih dan Tajdid PP Muhammadiyah. www.muhammadiyah.id @Lensamu @Muhammadiyah
[r]
Keluaran Jumlah Tenaga Pembersih Kantor 2 Orang Hasil Tersedianya Tenaga Pembersih Kantor 7,14%. Kelompok Sasaran Kegiatan