PENERAPAN METODE OPTIMASI MULTIRESPON MENGGUNAKAN HYBRID PCA-TAGUCHI DAN PCR- TOPSIS TAGUCHI PADA PENGGURDIAN MATERIAL KOMPOSIT
Teks penuh
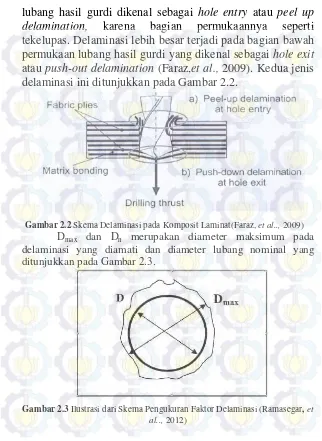
Gambar



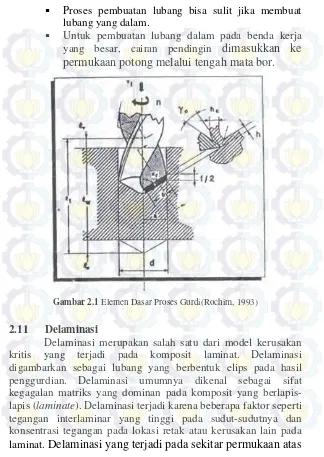
Dokumen terkait
• Click to edit Master text styles – Second level • Third level – Fourth level » Fifth level Best Practice Company ( Green Companies) Lely Riawati, ST, MT...
Tujuan penelitian ini secara umum adalah untuk mengetahui pelaksanaan metode cooperative learning pada pembelajaran bahasa dan sastra Indonesia dalam
SURABAYA PERSPEKTIF SOREN ABEY KIERKEGAARD” Jurusan Pemikiran Islam Program Studi Aqidah Dan Filsafat Islam Universitas Islam Negeri Sunan Ampel Surabaya. Skripsi ini
a) Editing yaitu mengatur tampilan media sedemikian rupa sehingga terlihat menarik. b) Validasi dilakukan untuk mengetahui dan memastikan bahwa media pembelajaran yang
Salah satu penelitian memakai kombinasi anestetik lokal bupivakain serta lidokain untuk mendapatkan hasil yang diinginkan, yaitu waktu awitan cepat dan lama kerja blokade
In their thesis, they intended to find out the quality of the English summative test for sixth grade students in
Berdasarkan data hasil penelitian tindakan kelas dengan penerapan model kooperatif tipe Make A Match dapat diambil simpulan bahwa penerapan pembelajaran kooperatif tipe
Perubahan suhu inti tubuh terjadi pada pasien perioperatif karena gangguan pada mekanisme termoregulasi yang dipengaruhi oleh beberapa faktor seperti jenis anestesi yang