PRINSIP MAKSIMUM PONTRYAGIN DALAM MODEL PENYEBARAN PENYAKIT SKRIPSI
Teks penuh
Gambar


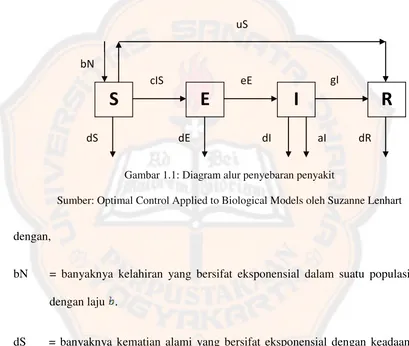

Dokumen terkait
Pada model ini, populasi dibagi menjadi 3 bagian, yaitu individu yang sehat tetapi rentan terhadap penyakit Tuberculosis yang disebut Susceptible , individu
Sehingga pada waktu tertentu kelompok individu rentan tidak memasuki individu I , semakin besar individu rentan yang tidak terjangkit penyakit maka kelompok
Pada model epidemik penyakit Campak ada dua cara yang dapat dilakukan untuk mencegah penyebaran penyakit yaitu dengan cara meminimalisir banyaknya penderita yang
Proses percabangan pada pola penyebaran penyakit adalah proses penyebaran penyakit dimana individu terinfeksi penyakit menginfeksi individu sehingga jumlah
Populasi pada model SEIQR dibagi menjadi lima kelompok yaitu, suspectible ( kelas subpopulasi yang rentan terinfeksi penyakit, latent ( kelas individu yang telah
[7] dengan menambahkan kompartemen populasi yang telah divaksin ( Vaccinated ), serta menganalisa dinamika penyebaran penyakit campak dengan melihat pengaruh proporsi populasi
Populasi pada model SEIQR dibagi menjadi lima kelompok yaitu, suspectible ( kelas subpopulasi yang rentan terinfeksi penyakit, latent ( kelas individu yang telah
Model Lipsitch merupakan perluasan dari model SEIR (susceptible-exposed-infected- recovered) yang memiliki populasi