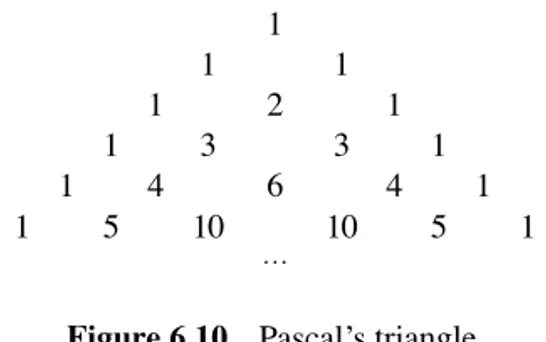
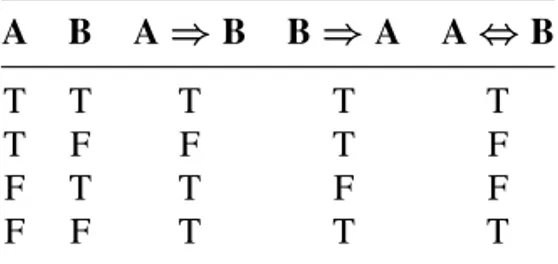
Discrete Mathemaitcs Demystified Free ebook download
Teks penuh
Gambar

Dokumen terkait
Pemerintah Kota dapat melakukan kerjasama antar Pemerintah Daerah Kabupaten/Kota atau melakukan kerjasama/bermitra dengan Badan Usaha dalam penyelenggaraan pengelolaan
Saya tidak ingin mendapatkan masalah dengan klien jika saya tidak memenuhi keinginan klien untuk berperilaku menyimpang dari standar profesional.. Saya khawatir jika klien saya
Diperlukan pengujian klasifikasi dengan menggunakan algoritme klasifikasi selain Fuzzy K-Nearest Neighbour atau Naïve Bayes untuk mengetahui apakah algoritme
Figure 7 shows the final process that displays 3D objects of molecular geometry on the smartphone android as a representation of the BrF 5 octahedral [17] The creation
Kedua-dua pesawat mempunyai persaingan dalam harga dan juga terdapat beberapa persamaan, antaranya Boeing 787 Dreamliner yang mutakhir dan Boeing 777 bersaing dengan Airbus
untuk mempermudah siswa sekolah dasar dalam memahami dan mengenal provinsi dibutuhkan suatu aplikasi edukasi yang dapat mengenalkan karakteristik dan nama ibukota dari
Skripsi yang berjudul “Uji Efek Stimulan Ekstrak Biji Cola ( Cola nitida A. Chev.) pada Mencit putih jantan” ini disusun dan diajukan untuk memenuhi persyaratan guna memperoleh
Dari berbagai pengertian diatas dapat disimpulkan bahwa tujuan laporna keuangan adalah menyediakan informasi posisi keuangan suatu perusahaan yang bermanfaat bagi