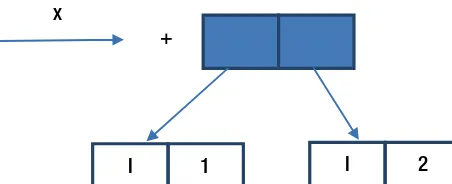
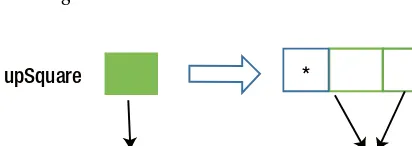
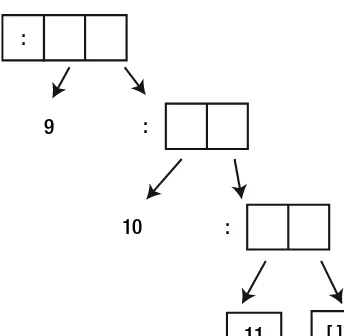
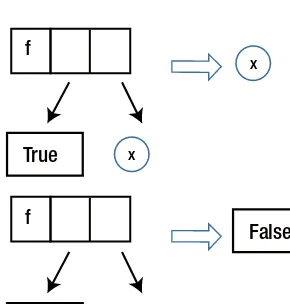
Practical Concurrent Haskell with Big Data Applications pdf pdf
Teks penuh
Gambar
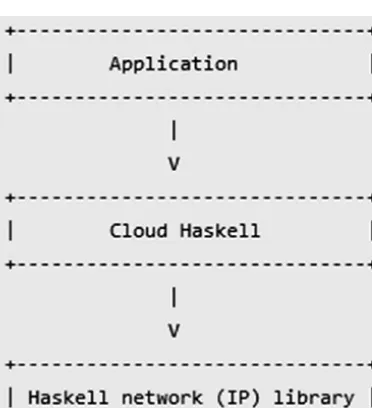
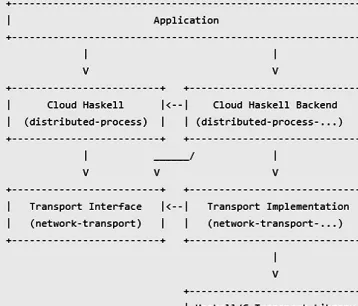
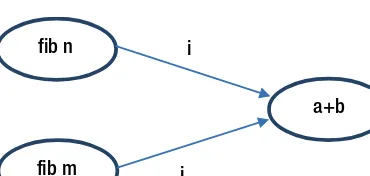
Dokumen terkait
Kunjungan serangga penyerbuk pada bunga pinang sangat minim, yaitu pada pinang Mongkonai 8 jenis serangga dengan jumlah serangga antara 0,6-129,2 serangga, pinang Huntu 13
Lirik lagu “Bibir” yang dipopulerkan oleh penyanyi Samantha Band adalah sebuah proses komunikasi yang mewakili seni karena terdapat informasi atau pesan yang
Permasalahan dalam penelitian ini adalah apakah penerapan model CTL dapat meningkatkan hasil belajar IPA materi hubungan antara sumber daya alam dengan lingkungan dan
CHAPTER IV FINDING OF THE RESEARCH 4.1 The Reading Comprehension of Recount Text of the Eighth Grade Students of SMP NU Al Ma’ruf Kudus in Academic Year 2012/2013
Atas dasar pemikiran di atas, maka perlu diadakan penelitian mengenai Faktor-Faktor Yang Mempengaruhi Pengambilan Keputusan Nasabah Dalam Memilih Produk Bank
Berbagai karakteristik banyak ditawarkan produsen ponsel dalam upaya untuk menarik pembeli, misalnya tentang kualitas produk yang dihasilkan, kemampuan dan
Table 3.. The body size also describes the uniqueness of the SenSi-1 Agrinak chicken as male line of native broiler chicken. Table 6 presents adult body weight and
Berdasarkan uraian tersebut diatas dapat disimpulkan semua kegiatan siswa baik di dalam kelas maupun di luar kelas yang mengarah pada peningkatan prestasi