View of PENERAPAN ALGORITMA HYBRID CROSS ENTROPY-GENETIC ALGORITHM DALAM PENYELESAIAN RESOURCE-CONSTRAINED PROJECT SCHEDULING PROBLEM
Teks penuh
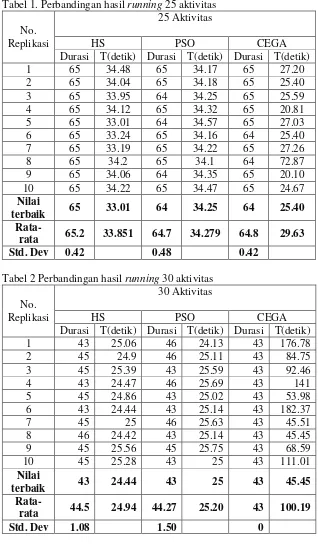
Gambar
Dokumen terkait
Tempat Uji Kompetensi (TUK) adalah suatu tempat yang memiliki sarana dan prasarana sesuai standar kompetensi yang telah ditetapkan untuk melaksanakan uji kompetensi melalui
Aktivitas esterifIkasi tertinggi pada alkohol dengan berbagai panjang rantai dimiliki butanol (13.04 nunol ALB/g prot.menit) yang berbeda nyata dengan aktivitas yang
Kampung Vascodanem, Memenuhi 28/A-SERT-VLK/XII/ 2014 Distrik Meyado, Kabupaten Teluk Bintuni Provinsi Papua Barat... Raya
Ketiga (3) sistem yang diterapkan oleh unit bagging dalam proses pengemasan pupuk urea yang dihasilkan pabrik, standar operating procedure (SOP) penggunaan mesin-mesin yang tersedia
Faktor pendukung dalam penerapan analisis jabatan di Kantor Kelurahan Gunung Telihan yaitu Undang-Undang Nomor 5 Tahun 2014 tentang ASN, kemudian Peraturan Menteri
Kegiatan yang dilakukan meliputi kegiatan rehabilitasi seperti konseling kesehatan agar orang tersebut lebih memahami tentang cara menjaga fungsi saluran kemih terutama ginjal
Hasil studi berupa model penjaminan mutu internal dapat digunakan untuk meningkatkan capaian standar nasional pendidikan, terdiri dari penetapan standar mutu acuan, penetapan
Tujuan yang akan dicapai adalah (1) Tujuan umum Penelitian ini bertujuan untuk mengetahui peningkatan kecerdasan visual spasial anak pada taman kanak- kanak melalui