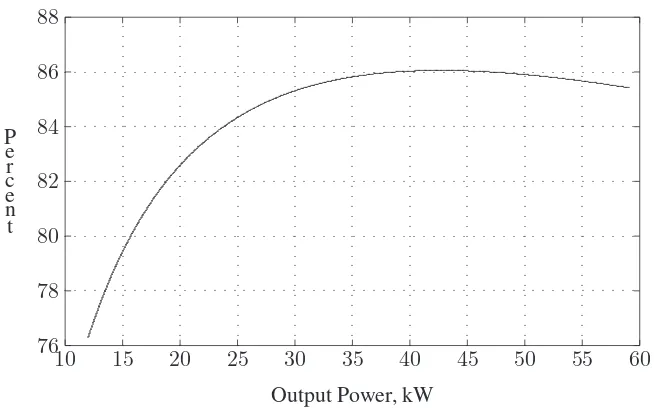
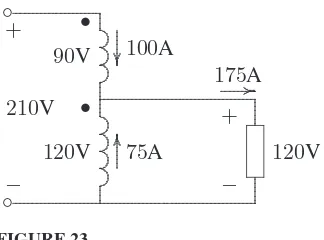
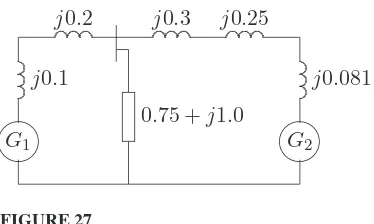
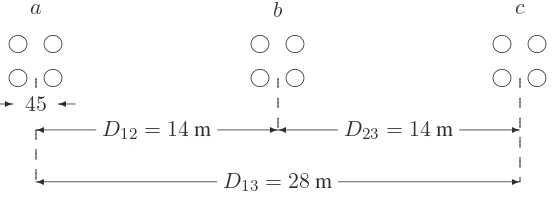
PSA Solution Manual Hadi Saadat
Bebas
285
0
0
Teks penuh
Gambar
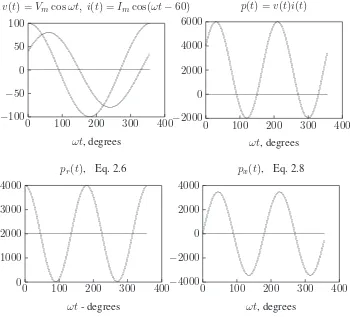
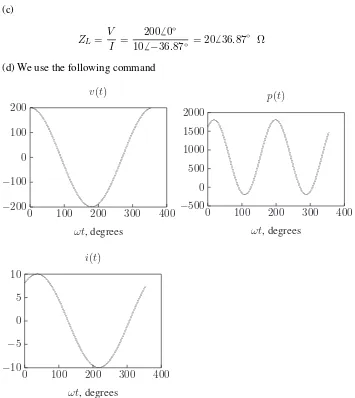
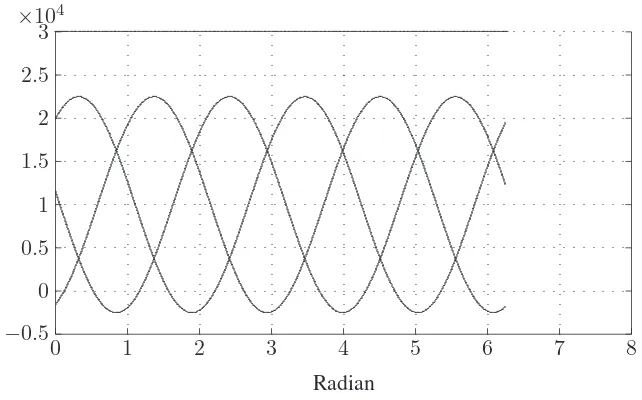
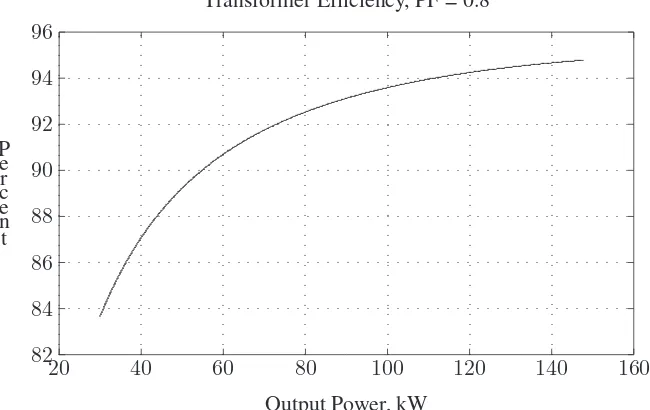
+7
Garis besar
Dokumen terkait