Data Science with Java Practical Methods for Scientists and Engineers pdf pdf
Teks penuh
Gambar

Dokumen terkait
A XML element text node is transformed in a JSON nested object when other types of nodes are present (see 6.1.3).. The XML element text value can be casted to a JSON object value
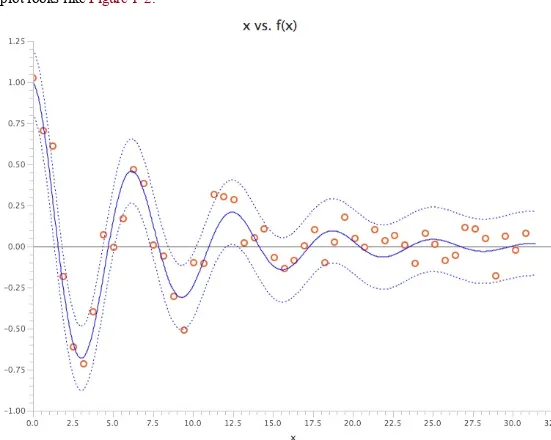
For our MapReduce job example, you can see in Figure 4.7 that the text is stored in different blocks on the data node. TextInputFormat
Aside from logs, analytics techniques, such as text analysis, which can be used to mine information from unstructured data sources, may also be useful?. For example, these
Chapter 17 will introduce the compose custom element and how it can be used in dynamic scenarios.. Chapter 18 will introduce creating
Data Science Using Java Data science Machine learning Supervised learning Unsupervised learning Clustering Dimensionality reduction Natural Language Processing Data science
f Keeping and representing data from a CSV file f Examining a JSON file with the aeson package f Reading an XML file using the HXT package f Capturing table rows from an HTML page..
■■ A static method parseClass (where Class is the name of the class, such as Byte or Integer ) that also accepts a string, and an optional radix to parse a string returns the
Assuming the only forces acting on the sphere are the resistive force and the gravitational force , let us describe its motion.1Applying New- ton’s second law to the vertical motion,