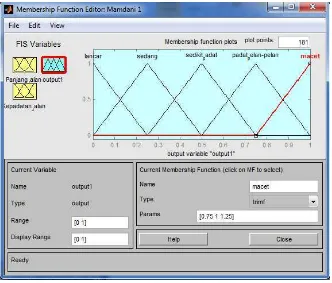
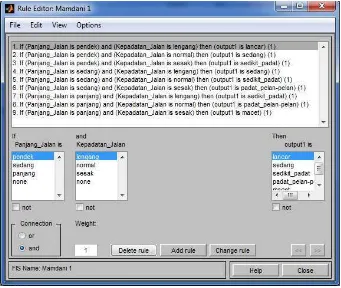
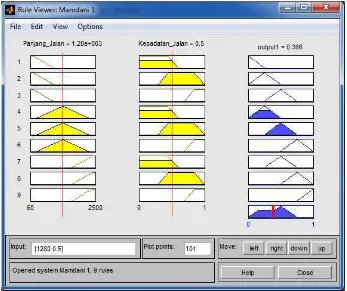
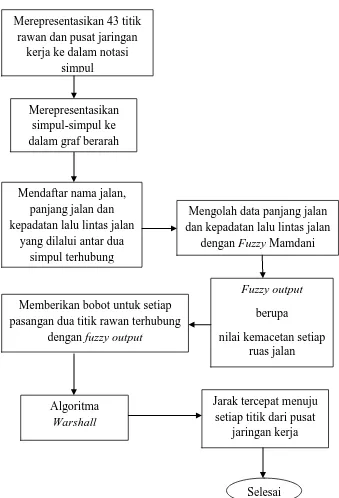
APLIKASI ALGORITMA HYBRID FUZZY-WARSHALL UNTUK MENENTUKAN RUTE TERCEPAT JARINGAN KERJA POLRES MAGELANG KOTA.
Teks penuh
Gambar

Dokumen terkait
Sedangkan tujuan khususnya adalah mengidentifikasi hambatan dan masalah sistem informasi dalam surveilans kesehatan ibu dan anak melalui SIP pada Desa Siaga,
OGC = -12,868 - 0,903AQ - 0,695ZScore + 6,710ALAG + € Hasil pengujian hipotesis pertama menunjukan bahwa variabel kualitas audit yang diproksikan dengan Kantor Akuntan Publik
Umumnya birokrasi hanya melihat proses pemantauan dan keberhasilan program dari sisi yang sangat materil, asumsi birokrasi yang penulis wawancarai menunjukkan asumsi bahwa jika
Dalam hal ini perlakuan III A rasio C : N-nya paling cocok untuk pertumbuhan konsorsium meskipun substrat atau sludge minyak bumi yang ditambahkan lebih sedikit Laju maksimum
Sel limfosit B akan melakukan proses pengidentifikasian terlebih dahulu terhadap antigen merupakan fungsi dari antibodi. Sel limfosit B juga mengalami proses
Biaya pembangunan suatu jaringan distribusi merupakan suatu persoalan yang memerlukan biaya cukup tinggi, untuk pengadaan suatu peralatan sistem
Puji syukur penulis panjatkan atas kehadirat Allah SWT yang telah melimpahkan rahmat, berkah serta hidayahNya sehingga penulis dapat menyelesaikan tesis dengan
Nurul Islam dalam waktu yang cukup panjang dari tahun 1932 hingga 1980 ini tentu mempunyai dampak terhadap masyarakat sekitar Kabupaten Ogan Ilir baik dari bidang