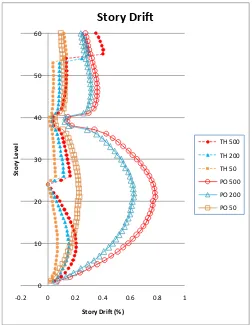
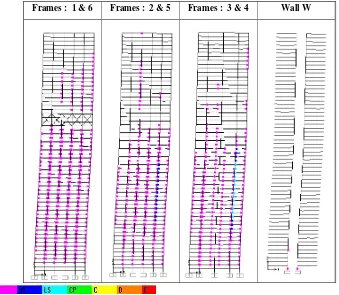
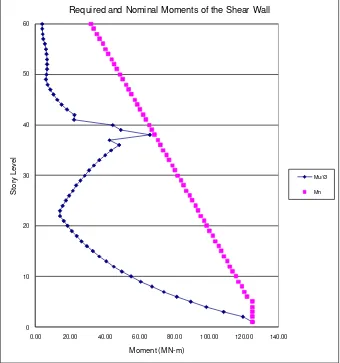
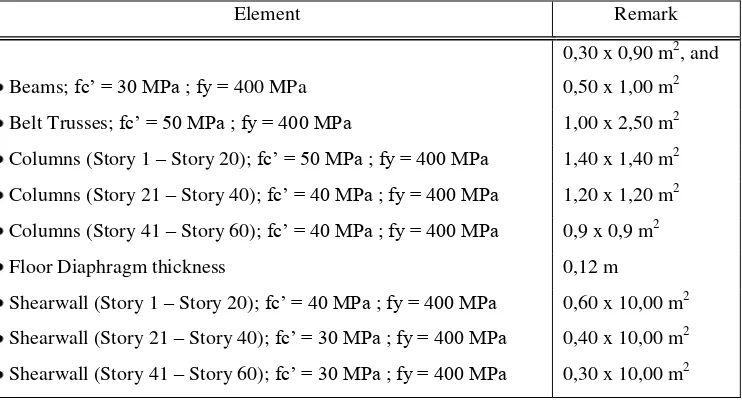
Belt Truss as Virtual Outrigger
Teks penuh
Gambar
![Figure 1. Tipical Belt Truss Location in a Highrise Building [1]](https://thumb-ap.123doks.com/thumbv2/123dok/1550695.2047436/2.595.80.512.385.471/figure-tipical-belt-truss-location-highrise-building.webp)
![Figure 3. The 30-Story SFBT Building Considered by Pudjisuryadi and Lumantarna [5,6]](https://thumb-ap.123doks.com/thumbv2/123dok/1550695.2047436/3.595.120.491.170.436/figure-story-sfbt-building-considered-pudjisuryadi-lumantarna.webp)

Dokumen terkait
22 It appears that the account is Vaulin’s for a number of reasons, including: (1) the account was registered November 20, 2010, in the name “Artem Vaulin” with an address located in
Microbial biomass (assayed by chloroform fumigation – extraction) nearly doubled in surface (0 – 5 cm) mineral soils in response to earthworm activity, an effect that
Dengan demikian menurut penulis dapatlah dipahami, bahwa tanggung jawab suami terhadap nafkah keluarga yang didasarkan atas pernikahan sirih, pertama; dalam
Fakultas Ekonomi Universitas Sumatera Utara Medan lebih berorientasi pada pelayanan pendidikan yang bermutu dan berkualitas, melakukan penelitian- penelitian yang bermanfaat bagi
Seorang individu dengan pengelolaan keuangan yang kurang baik akan.. menimbulkan sikap untuk
nclusion from the table or figure which answers the “So what?”
Three-step interview technique was implemented in experimental group, while the control group was treated with conventional technique of teaching.. In collecting data,
Dapat disimpulkan bahwa, teknik pembelajaran opini teman merupakan sebuah teknik pembelajaran yang digunakan atau diterapkan oleh seorang guru untuk memecahkan