102 Jurnal Ilmu Komputer dan Informasi (Journal of Computer Science and Information)
Teks penuh
Gambar

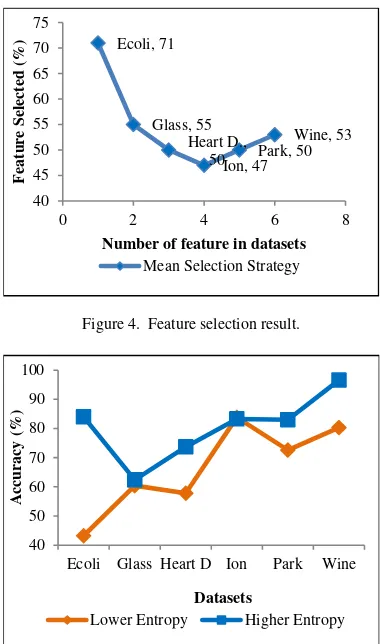
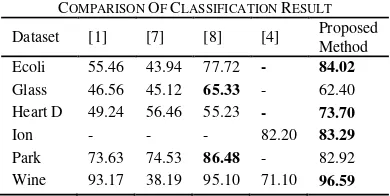
Dokumen terkait
Mengingat konsep Ilmu Ekonomi sebagai tolak ukur kajian pertumbuhan ekonomi yang sudah terlanjur diyakini serta diterapkan secara luas, maka kita tidak boleh ketinggalan dan mau
Dimana inovasi adalah ide, praktik atau objek yang dipersepsikan sebagai sesuatu yang baru oleh individu atau oleh unit yang mengadopsinya. Kebaruan suatu inovasi
Survival after cardiac arrest is most likely to be the outcome in the following circumstances: when the event is witnessed; when a bystander summons help from the emergency services
Mungkin orang yang kita hormati atau yang lebih senior meminta kita melakukan sesuatu, padahal pada waktu yang bersamaan kita sedang ataau akan melakukan suatu pekerjaan., akan
· Kebun pohon induk adalah kebun yang ditanami dengan beberapa varietas buah unggul untuk sumber penghasil batang atas (mata tempel atau cabang entres) untuk perbanyakan dalam
Another strategy is the use of topical retinoids to maintain clearing once anti- biotic therapy has suppressed the inflammatory phase of acne and possibly to consider
Penataan ruang sebagai suatu sistem perencanaan tata ruang, pemanfaatan ruang, dan pengendalian pemanfaatan ruang merupakan satu kesatuan yang tidak terpisahkan antara yang satu
[r]