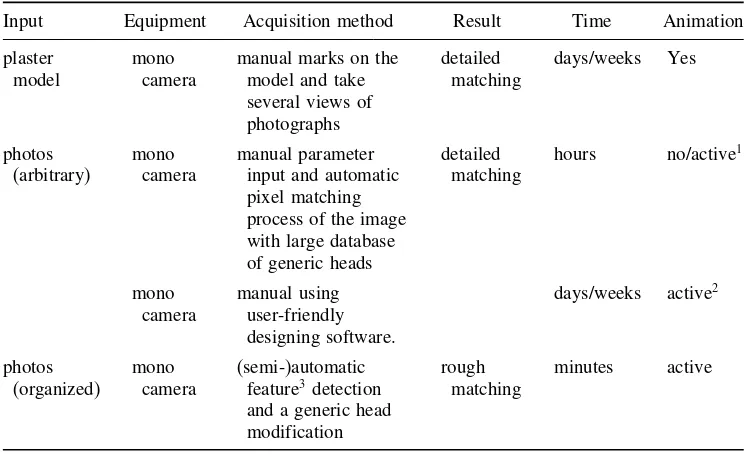
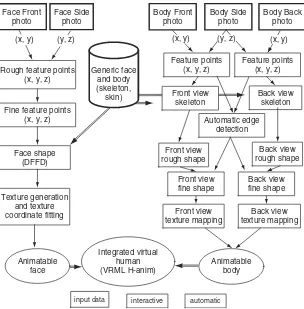
Handbook Of Virtual Humans pdf
Teks penuh
Gambar




Garis besar
Dokumen terkait
Dengan Hormat, Bahwa dalam rangka proses Evaluasi Dokumen Kualifikasi dan Pembuktian Kualifika perusahaan yang telah mengupload dokumen kualifikasi untuk Pekerjaan Jasa
This research, focused on students’ problem at the eighth grade students of SMP Negeri 1 Kulawi in improving their vocabulary mastery covering meaning, spelling
1) Pendahuluan: memuat latar belakang dan tujuan praktikum. 2) Tinjauan Pustaka: memuat teori praktikum yang telah diketahui hingga saat ini. 3) Alat, bahan dan cara kerja:
Apabila ada sanggahan dari peserta untuk kegiatan tersebut diatas terhadap peserta lelang agar dialamatkan kepada :.. - Panitia Pengadaan Barang/Jasa Dishubkominfo Kota Sabang
RENCANA UMUM PENGADAAN BARANG / JASA DINAS KESEHATAN KOTA SEMARANG.. TAHUN
Sebagaimana telah diuraikan di atas, sarana pembelajaran untuk mencapai kompetensi dalam PBP menggunakan tugas proyek sebagai model pembelajaran. Para peserta
1) Melaksanakan Kegiatan Supervisi secara umum, Supervisi lapangan, koordinasi dan inspeksi kegiatan-kegiatan pembangunan agar.. pelaksanaan teknis maupun administrasi
Tugas Supervisi secara umum adalah mengawasi kelancaran pekerjaan pembangunan yang dikerjakan oleh Rekanan/Kontraktor pelaksana, yang menyangkut kuantitas,