Beginning Blockchain A Beginner's Guide to Building Blockchain Solutions pdf pdf
Teks penuh
Gambar

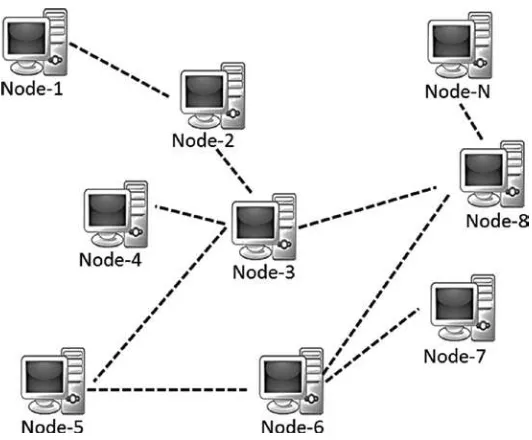

Dokumen terkait
Energy is not a nutrient but is derived from most parts of the feed. Cows use energy to function (breathe, walk, graze, gain
You don´t need to be an accomplished athlete in order to be able to enjoy the unique sensation of swooping through the air that only hang gliding can bring.. As long as you
Although the filler makes up for the weight between different balls the two most important parts of a bowling ball are actually the core and the coverstock.. The shape of a
You can recommend affiliate products (basically selling other people´s stuff for a commission) on content sites. You can sell advertising on a busy site. Product Sales Sites?. This is
To help overcome this problem, this chapter provides a brief overview of several Java features, including the general form of a Java program, some basic control structures, and
When a Licensee is involved in a transaction or series of transactions for the receipt, exchange, conversion, purchase, sale, transfer, or transmission of Virtual Currency, in
They take information of a transaction as an input and then verify the whole information whether it is cryptographically accurate or not, compute the new hash, create a new block,
Transactions not settled at the reporting date If a transaction is not settled before the end of a reporting, then: i record the transaction in the functional currency at the spot