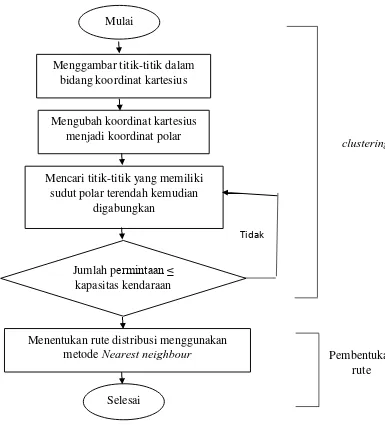
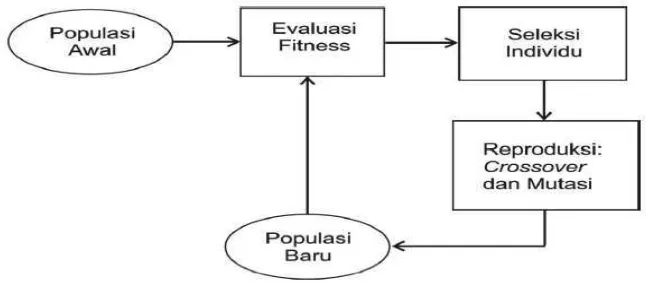
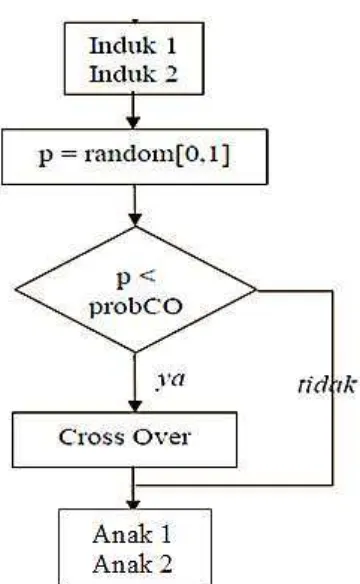
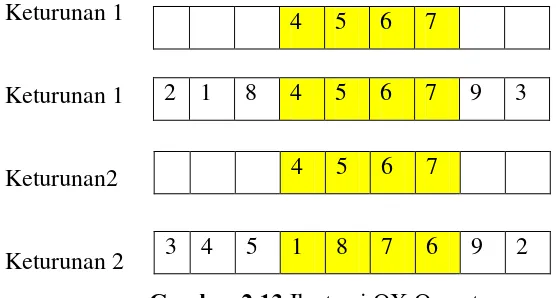
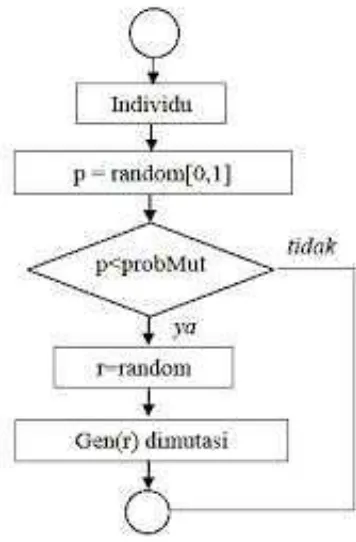
PENERAPAN ALGORITMA GENETIKA DAN ALGORITMA SWEEP PADA PENYELESAIAN CAPACITATED VEHICLE ROUTING PROBLEM (CVRP) UNTUK OPTIMASI PENDISTRIBUSIAN GULA.
Teks penuh
Gambar
Dokumen terkait
Problematika ekonomi manusia dalam perspektif Islam adalah pemenuhan kebutuhan (need) dengan Sumber Daya Alam (SDA) yang tersedia, dengan adanya konsep maslahah
Indikator Kinerja Utama (IKU) Dinas Kesehatan tahun 2013-2018, yang tertuang dalam dokumen RPJMD Kota Sukabumi tahun 2013-2018 ditetapkan berdasarkan Keputusan
Bagian Keuangan / Umum selaku pembantu Kepala Wilayah bertanggung jawab menyusun rencana dan melaksanakan kegiatan pengelolaan keuangan, fungsi kebendaharaan, penyusunan
Sedangkan berdasarkan penelitian Dian (2011) dengan menggunakan metode dilusi tabung untuk mengetahui KHM dan KBM dengan menggunakan ekstrak daun kersen dengan etanol
Sebagian besar DKI Jakarta kecuali bagian Utara dan Timur Laut, Sebagian besar Kab Tangerang kecuali bagian Tengah dan Barat, Seluruh Kota Tangerang dan Kota Tangerang
Sebagian besar DKI Jakarta kecuali bagian Timur Laut, Seluruh Kab Tangerang, Kota Tangerang, Kota Tangsel, Kab Serang kecuali sebagian kecil di bagian Utara, Kota Cilegon,
Dalam analisis hidrologi dilakukan beberapa analisis yaitu analisis curah hujan rerata daerah, analisis kerapatan stasiun hujan, analisis jarak antar stasiun dan analisis
Pola angin di Indonesia secara umumnya menunjukkan pola angin baratan, hal tersebut terlihat dari nilai suhu muka laut yang berimplikasi dari adanya variasi pola tekanan udara