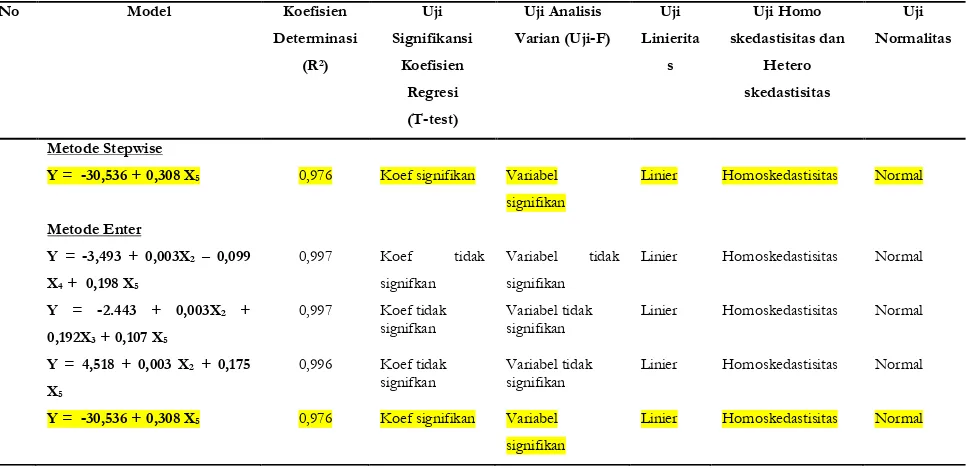
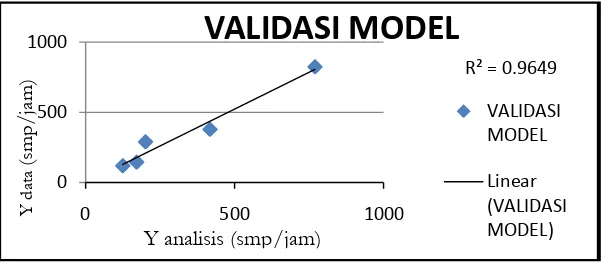
ANALISIS MODEL TARIKAN PERGERAKAN PADA RUMAH SAKIT (STUDI KASUS DI DAERAH ISTIMEWA YOGYAKARTA)
Teks penuh
Gambar



Dokumen terkait
dapat dilihat dari desain politik hukum yang dibuat oleh negara yang dirumuskan dalam konstitusi, politik legislasi melalui prolegnas dan desain kebijakkan pemerintah dalam
Kawasan sekitar Tahura Djuanda umumnya merupakan dataran tinggi yang memiliki keindahan panorama (scenic beauty) dan lingkungan alami cukup asri sehingga mendorong
Pengantar Ilmu Kesejahteraan Sosial, Metode-Metode Pekerjaan Sosial, Sistem Sosial Indonesia, Metode Penelitian Sosial, Lembaga-Lembaga Pembangunan, Teori Sosiologi
Perlu diketahui, perosoalan sumber keuangan desa sebelumnya bersumber dari (APBD), bahkan peraturan perundangan- undangan seperti Peraturan Pemerintah Nomor 72 tahun
Hasil analisis menunjukkan bahwa ada interaksi antara media pembelajaran dengan kemampuan awal siswa terhadap keterampilan membaca nyaring; media pembelajaran slide
Kata sandang yang diikuti oleh huruf qamariyah ditransliterasikan sesuai dengan aturan yang digariskan di depan dan sesuai pula dengan bunyinya. Huruf sandang
Jika kalian menjalankan pemerintahan sesuai dengan yang diridhai Allah, kalian perbaiki berbagai keadaan di negeri kalian dengan syariat Islam, maka umat ini akan terjaga dari