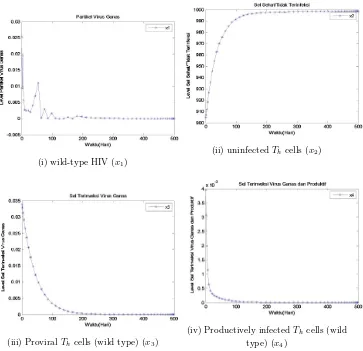
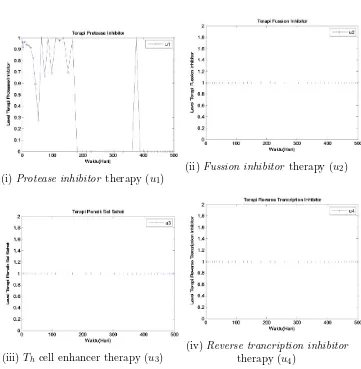
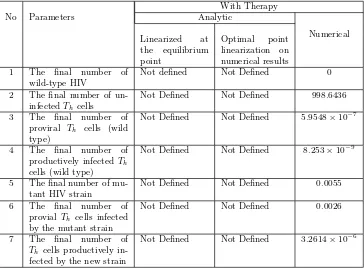
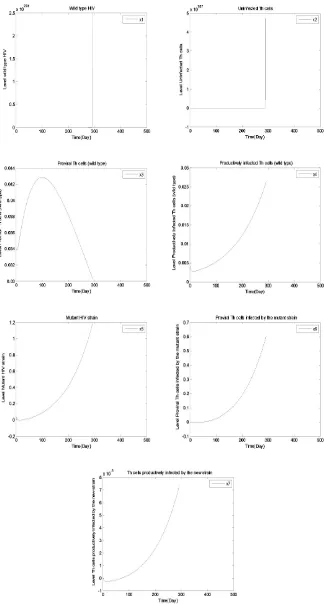
THE SIMULATION OF CONTROLING THE SPREAD OF HIV USING ANALYTICAL AND NUMERICAL APPROACH
Teks penuh
Gambar

![Table 1: Initial Condition Variable State [11]](https://thumb-ap.123doks.com/thumbv2/123dok/3550014.1778815/14.595.163.433.132.404/table-initial-condition-variable-state.webp)
Dokumen terkait
sosial terutama bagi masyarakat yang menduduki kelas bawah seperti buruh. Peranan orang tua sangatlah penting dalam mewujudkan pendidikan tinggi bagi. anak, nilai-nilai yang
(3) Dalam hal penanggung jawab usaha dan/atau kegiatan yang melakukan pemanfaatan Ekosistem Gambut tidak memenuhi ketentuan dalam pembekuan izin lingkungan sebagaimana
The Role of Urban Marketing in The Local Economic Development.Theoritical and Empirical Researches in Urban Management. Statistik Nonparametris
- Calon Penyedia barang dan jasa yang telah mendaftar pada paket pekerjaan. Pemagaran Gedung Kantor dan ikut secara on line di
[r]
[r]
Sehubungan dengan Pel el angan Pemil ihan Langsung Pekerj aan Peningkat an Jal an Pat t imura Kot a Muara Sabak Kabupat en Tanj ung Jabung Timur Tahun Anggaran 2014, unt uk Paket
Konversi Biomassa Limbah Kulit Durian (Durio Zibhetinus Murray) Menjadi 5- Hidroksimetilfurfural Dalam Larutan Zncl2 Menggunakan Katalis Crcl3.. Universitas Pendidikan Indonesia