Mhr Mengem Kemampuan Mtk SMA MA IPA Kelas 11 Wahyudin Djumanta R Sudrajad 2008
Teks penuh
Gambar
Dokumen terkait
Tabel 4.2 : Distribusi Frekuensi Kemampuan Menulis Cerpen Pada Siswa Kelas X SMA Swasta Alhidayah Medan TP 2014/2015 Sebelum Menggunakan Model Pembelajaran Contextual
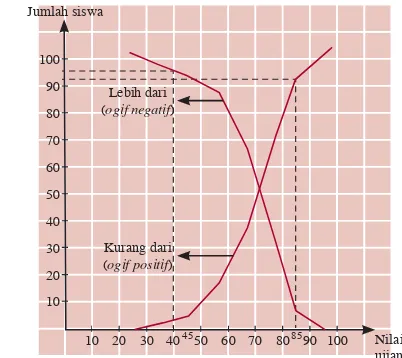
Tabel distribusi frekuensi kumulatif kurang dari merupakan tabel yang mencakup daftar jumlah frekuensi semua nilai yang kurang dari atau sama dengan nilai tepi atas pada setiap
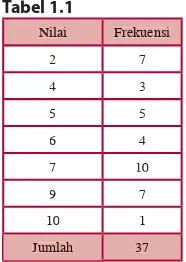
Perhatikan interval-interval pada Tabel 1.5. Interval-interval tersebut dibatasi oleh dua bilangan yang merupakan batas dari interval. Bilangan di sebelah kiri setiap interval
Tabel 4.7 Distribusi Frekuensi dan Persentase Tingkat Kemampuan Penalaran Siswa Kelas Eksperimen dan Kontrol
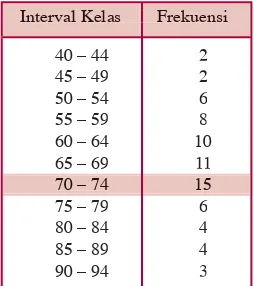
1. Menentukan tabel distribusi frekuensi a.. Dengan demikian jumlah interval kelas adalah 6,18 dibulatkan menjadi 6.. Dari hasil perhitungan di atas diperoleh nilai
Distribusi frekuensi perolehan skor variabel persepsi terhadap layanan bimbingan belajar yang ditentukan dalam delapan kelas interval disajikan pada tabel 1, sedangkan frekuensi skor
lebih jelasnya dapat dilihat pada tabel berikut: Tabel 4.4 : Distribusi Frekuensi siswa Kelas III SDN 109 TUARA Kecamatan Enrekang Kabupaten Enrekang Interval Presentasi Belajar
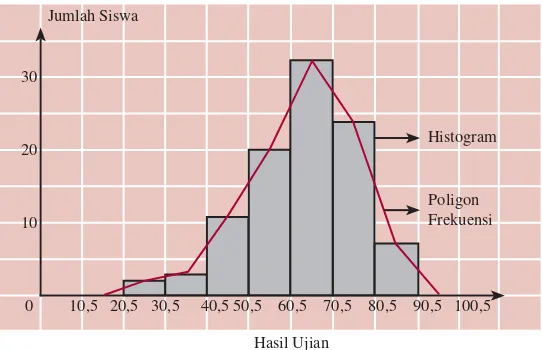
Membaca Data dalam Bentuk Tabel dan Diagram 2.2 Menyajikan Data dalam Bentuk Tabel Distribusi Frekuensi dan Histogram 2.3 Beberapa Pengertian Dasar dalam Statistika 2.1 Ukuran