OPTIMASI SEBARAN TITIK GCP DAN ICP PADA PROSES ORTOREKTIFIKASI CITRA RESOLUSI TINGGI UNTUK PEMBUATAN PETA SKALA 1:5.000 (STUDI KASUS: 1 SCENE CITRA PLEIADES 033 LUMAJANG)
Teks penuh
Gambar
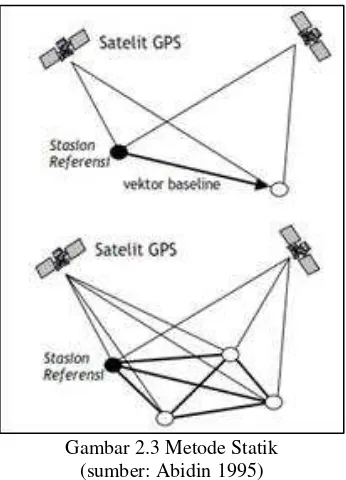

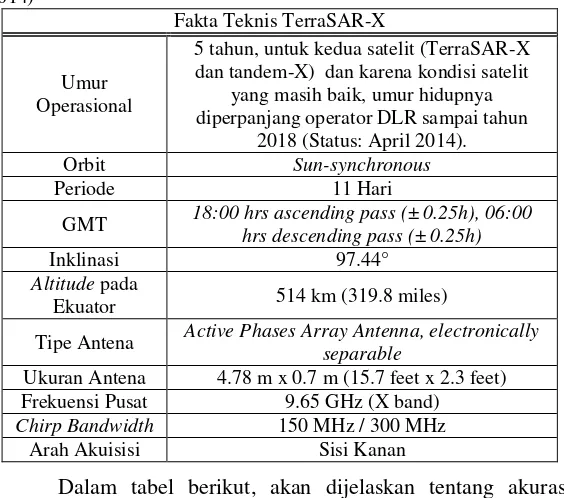
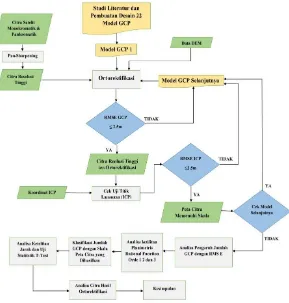
Dokumen terkait
Pemfaktoran ini dilakukan untuk memperoleh kunci privat yang dapat digunakan untuk memperoleh pesan asli (plaintext). RSA digunakan untuk proses enkripsi dan
Buku ini memuat naskah hasil penelitian dari berbagai bidang kajian yang telah dipresentasikan pada Seminar Riset Teknologi Informasi (SRITI) 2016.. Seminar Riset Teknologi
Melihat pentingnya upaya dalam upaya pelestarian warisan budaya maka dilakukan dengan suatu cara yang dapat memperkenalkan dan sebagai media pembelajaran akan suatu warisan
Jika user menjawab pertanyaan salah, sistem akan memberikan hint untuk user agar dapat menjawab dengan benar... Gambar 12
pembekalan materi, dan pelatihan keterampilan bermain softball melalui kegiatan praktek lapangan. Pada akhir program dilakukan evaluasi kepada setiap peserta untuk
Apabila field btnPlay masih null atau belum diinisialisasi maka field btnPlay akan diinisialisasi dengan memanggil method Find dari kelas GameObject, dimana GameObject yang
Siswa diberikan stimulus berupa pemberian materi oleh guru (selain itu misalkan dalam bentuk lembar kerja, tugas mencari materi dari buku paket atau buku-buku
Saraf yang mensistesis dan melepaskan ACh disebut saraf kolinergik, yakni saraf praganglion simpatis dan parasimpatis, saraf pasca ganglion parasimpatis dan saraf