PADA SIRIP 3 DIMENSI KEADAAN TAK TUNAK ” TUGAS AKHIR - Laju perpindahan kalor dan efektivitas pada sirip 3 dimensi keadaan tak tunak - USD Repository
Teks penuh
Gambar
Dokumen terkait
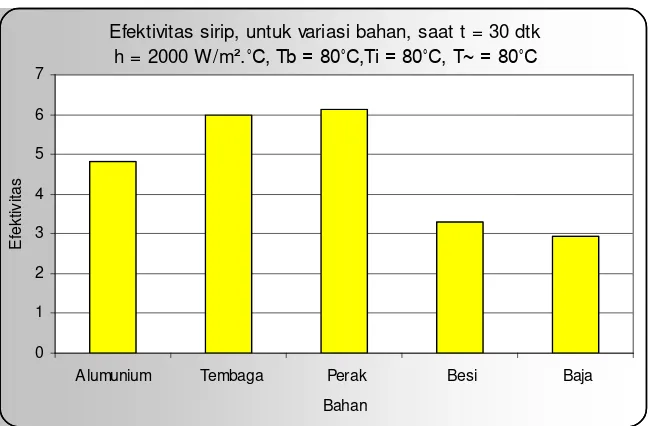
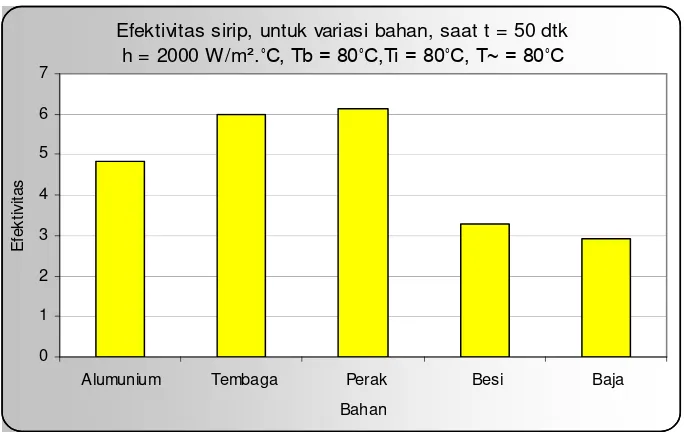
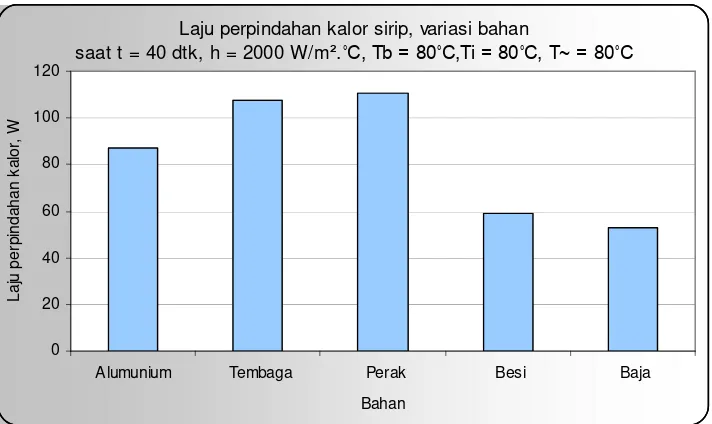
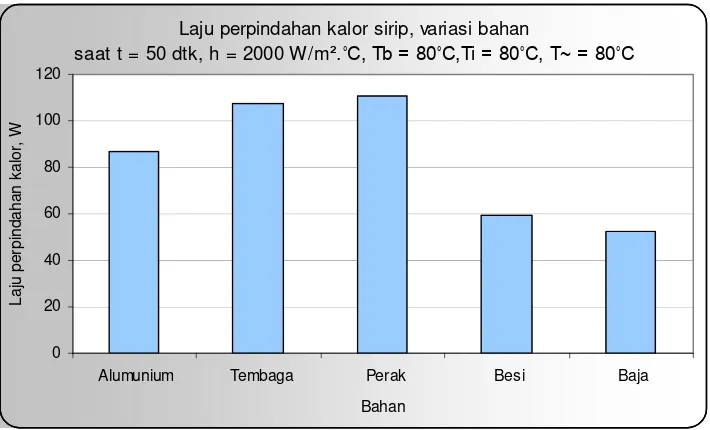
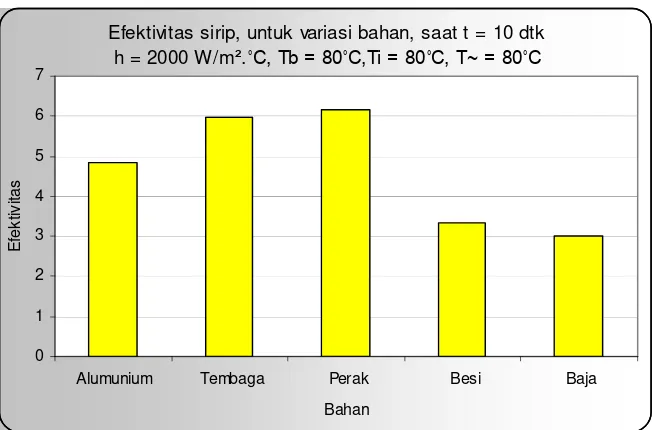
Dari grafik perbandingan laju aliran kalor untuk semua bahan dengan waktu yang sama serta harga h yang sama seperti yang disajikan di atas, dapat dikatakan bahwa besarnya laju
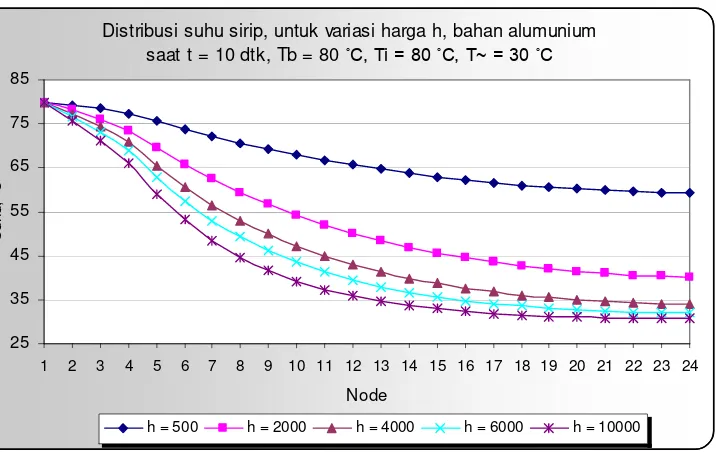
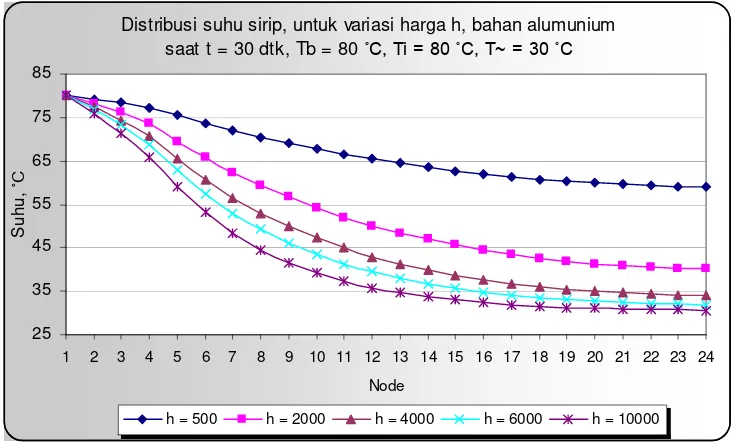
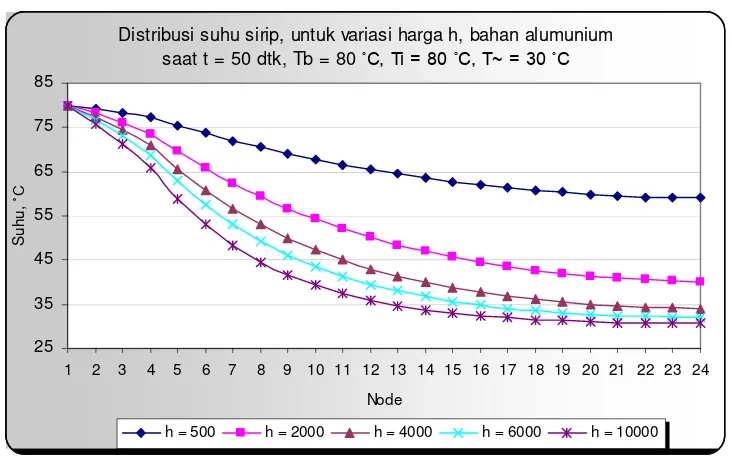
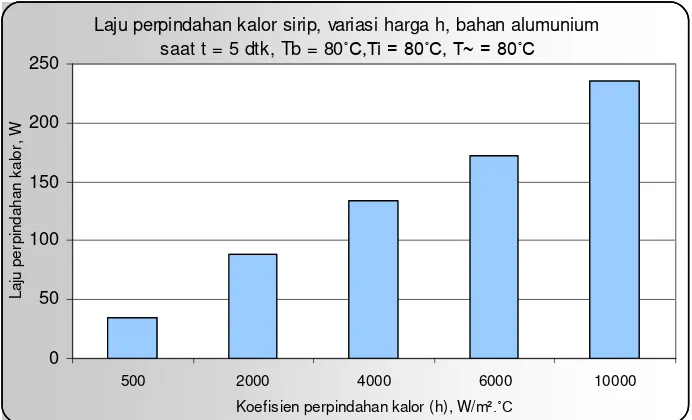
Dari hasil perhitungan dan analisa pembahasan yang telah dilakukan dapat disimpulkan bahwa untuk nilai koefisien perpindahan panas konveksi 50 W/m 2 o C (a) waktu
a) Penelitian ini dapat memberikan wawasan baru tentang perhitungan laju perpindahan kalor, efisiensi dan efektivitas sirip 2D pada keadaan tak tunak untuk sirip
Penelitian ini bertujuan untuk : (1) Mengetahui pengaruh bahan terhadap distribusi suhu, laju perpindahan kalor dan efektifitas pada sirip berbentuk kerucut terpotong pada keadaan
perpindahan kalor, efisiensi, dan efektivitas sirip kerucut dengan diameter sebagai fungsi posisi pada keadaan tak tunak serta memvariasikan nilai koefisien perpindahan
a) Penelitian ini dapat memberikan wawasan baru tentang perhitungan laju perpindahan kalor, efisiensi dan efektivitas sirip 2D pada keadaan tak tunak untuk sirip
Penelitian ini bertujuan untuk mengetahui distribusi suhu dari waktu ke waktu dan laju perpindahan kalor yang terjadi pada pan mould hosti kasus 3 dimensi keadaan tak
Penelitian ini bertujuan untuk mengetahui pengaruh bahan sirip dan pengaruh nilai koefisien perpindahan kalor konduksi terhadap waktu yang diperlukan sirip untuk mencapai