BILANGAN RAMSEY UNTUK GRAF BINTANG S
Teks penuh
Gambar
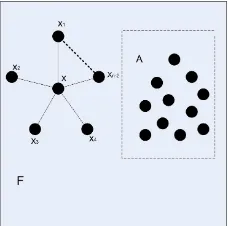
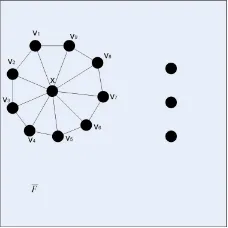
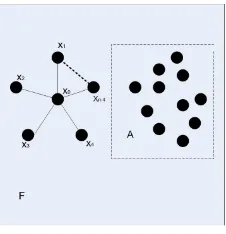
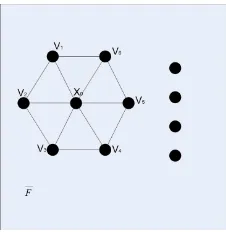
Dokumen terkait
Pada triwulan II-2013, jumlah aliran uang tunai yang masuk ke kas Bank Indonesia yang berasal dari setoran perbankan di NTB masih berada pada tren peningkatan yang
dan menarik untuk anak usia dini. Oleh karena itu, peneliti akan mencoba.. menggunakan metode pembelajaran yang berbeda yaitu dengan menggunakan. media papan
Puji syukur tercurahkan atas rahmat Allah SWT, sehingga penulis dapat menyelesaikan penyusunan Tugas Akhir Analisa Neraca Air DAS Logung yang merupakan syarat
Karena dalam kurun waktu tersebut seperti menjadi masa gelap dimana produk jadi jumlahnya kurang dari target yang sudah ditentukan, dan pasti adanya lembur untuk
Variable LDR, IPR, NPL, IRR, BOPO and FBIR in a partially manner had no significant influence, NPL had a significant influence,LDR, IPR, IRR, BOPO and FBIR had no
Ternyata FGD memperkuat hasil analisis Matrik Pertumbuhan dan Kontribusi yang menempatkan sektor perdagangan, hotel dan restoran berada pada posisi prima sehingga
Pada hari ini Selasa tanggal lima belas bulan Agustus tahun Dua Ribu Tujuh Belas. (15-08-2017), sesuai dengan jadwal yang termuat pada portal
Peradilan Agama dalam perkara Ekonomi syariah, Jakarta, Rajawali Press, 2011 13 Mahasiswa mengenal dan mengamati langsung praktek mediasi di Pengadilan Agama Praktek