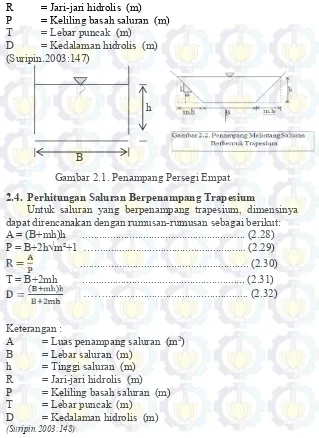
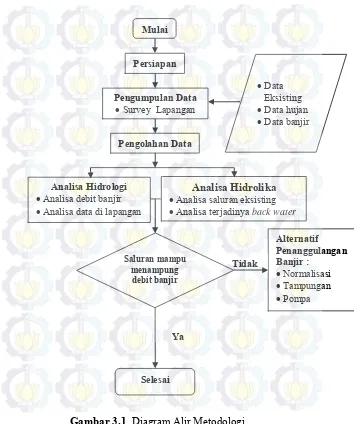
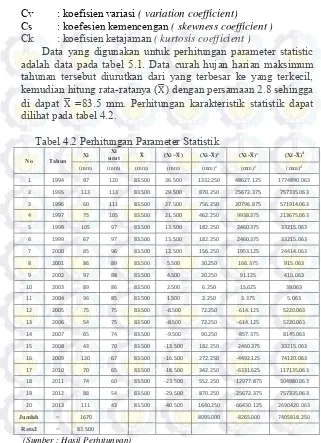
Pengendalian Banjir Di Kecamatan Gresik - ITS Repository
Teks penuh
Gambar



Dokumen terkait
Penyajian pada perancangan media informasi ini dengan membentuk objek dan pengaturan tata letak dengan menggunakan Adobe Illustrator yang disesuaikan dengan
Demikian juga dengan arus kas operasi yang juga tidak berpengaruh signifikan terhadap dividend payout ratio yang diperlihatkan dari hasil uji statistik t
Furthermore a short consideration related to the orthophoto generated using a traditional semi- automatic digital photogrammetric software (LPS from Leica): as it
Pada lama waktu thawing yang sama, motilitas spermatozoa pada semen beku sapi FH yang di- thawing dalam air 37°C memiliki kecenderungan lebih tinggi jika dibandingkan dengan
03 Jumlah rekomendasi kebijakan teknologi industri 04 Jumlah hasil litbang yang siap diterapkan.. 2 05 Jumlah kerja sama yang
Untuk memenuhi kebutuhan informasi pelayanan kepada masyarakat, setiap unit pelayanan instansi pemerintah wajib mempublikasikan mengenai prosedur, persyaratan, biaya,
Didapatkan faktor internal berupa usia 64 tahun, gender : perempuan, lansia, pengetahuan pasien mengenai DM masih kurang, sering minum obat tidak sesuai jadwal, riwayat
Melihat hasil ini sebenarnya kurang cukup memberikan informasi lebih lanjut tentang penye- bab responden bersikap negatif pada dua per- tanyaan yang dimaksudkan, hanya saja