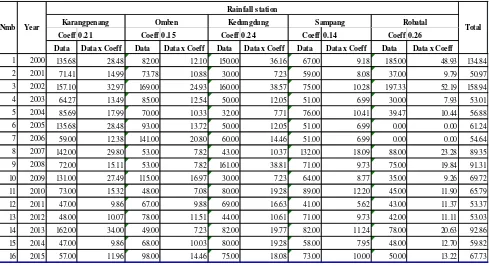
The Influence of Basin Landuse Coverage to Flood Hazard at Kemoning River, Kabupaten Sampang
Teks penuh
Gambar



Dokumen terkait
Panitia memberikan kesempatan kepada peserta lelang untuk menyampaikan sanggahan Kepada Kepala Bidang SDK dan Pengembangan Kesehatan selaku Pejabat Pembuat Komitmen
WAKIL PIMPINAN REDAKSI : Dr. I Wayan Sudarsana, S.Si., M.Si. Kimia FMIPA Univ. Biologi FMIPA Univ. Made Pharmawati, M.Sc., PhD. Biologi FMIPA Univ.dayana). Keahlian:
Sehubungan dengan proses Lelang Pemilihan Langsung Paket Pekerjaan Pembangunan Pusat Kesehatan Hewan (Puskeswan) Pada Dinas Kelautan Perikanan Pertanian dan Ketahanan Pangan Kota
[r]
Ada hubungan yang sangat signifikan antara aspek heuristik dalam memandang dan menghadapi suatu permasalahan dalam kehidupan dengan aspek persepsi antar kelompok
Pada siklus 1 nilai siswa yang mencapai ketuntasan adalah 15 siswa (41,66%) dengan presentase minat belajar siswa sebesar 49%, kemudian pada siklus 2 mencapai sebanyak 29
Terlaksananya Fasilitasi keikutsertaan Pameran Kota Tangerang 2 kali dan Pameran Hari Pangan sedunia atau Flori dan Flora Nasional 2015 (PF2N) 1 kali. Kota Tangerang Promosi
2) Tahapan-tahapan apa saja yang anda lakukan berkaitan dengan upaya membatasi paparan pasien terhadap infeksi yang berasal dari pengunjung? 3) Apa hambatan