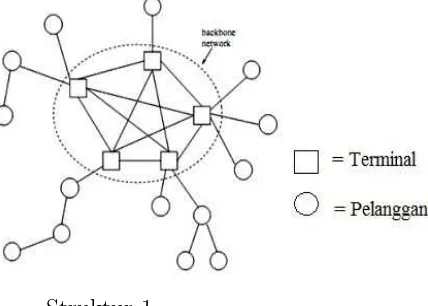
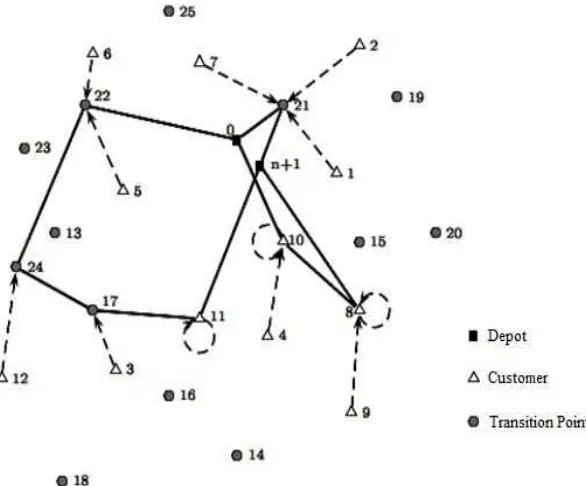
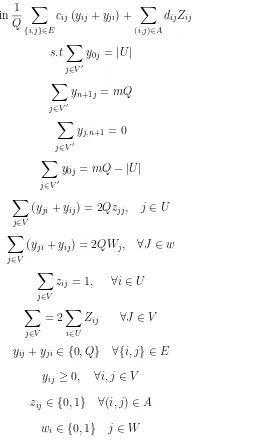BAB 2 TINJAUAN PUSTAKA - Metode Variable Neighborhood Search (VNS) pada Persoalan m-Ring Star Berkapasitas
Teks penuh
Gambar
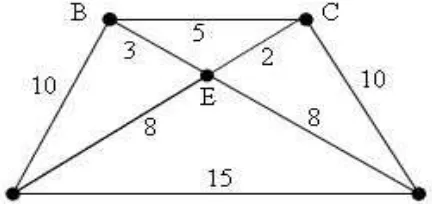
Dokumen terkait
〔下級審民訴事例研究八〇〕遺産分割調停事件の相手方が税務署長に対して提出した相続税申告
Dengan pertimbangan responden dalam penelitian ini adalah anggota Polda Sumut dan mempertimbangkan berbagai peraturan yang terkait, maka karakteristik anggaran yang
Masyarakat pekerja di kota-kota besar seperti Jakarta sebagian besar merupakan pekerja yang selalu disibukkan dengan deadline penyelesaian tugas akhir, tuntutan yang
Puji syukur dan terima kasih Penulis panjatkan ke hadirat Tuhan Yang Maha Esa karena berkat dan rahmat-Nya yang berlimpah, maka Penulis dapat menyelesaikan penulisan skripsi
Karya ilmiah yang ditulis oleh Susanto dengan tujuan untuk mengetahui pengaruh rasio likuiditas, profitabilitas, solvabiitas dan ukuran perusahaan terhadap harga pasar
Di bidang pencegahan agar seseorang tidak jatuh dalam keadaan stres, cemas, dan atau depresi maka sebaiknya kekebalan yang bersangkutan perlu ditingkatkan agar mampu
Hal tersebut tidak sejalan dengan penelitian Oktaviani, et al bahwa asupan zat gizi makro dan juga energi pada fast food dapat mempengaruhi status gizi para
Penelitian ini dilaksanakan melalui beberapa proses tahapan diantaranya adalah persiapan bahan baku limbah ebi, persiapan larutan yang akan digunakan selama penelitian,