BAB II KAJIAN PUSTAKA A. JARINGAN SYARAF TIRUAN 1. Definisi Jaringan Syaraf Tiruan - OPTIMALISASI JARINGAN BACKPROPAGATION DITINJAU DARI JUMLAH NEURON DALAM LAPISAN TERSEMBUNYI - repository perpustakaan
Teks penuh
Gambar
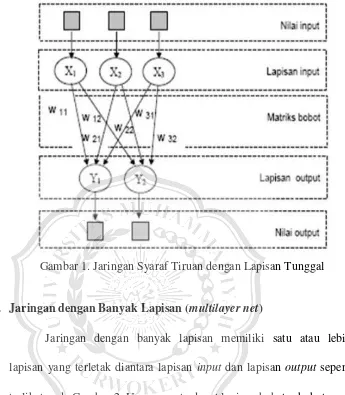
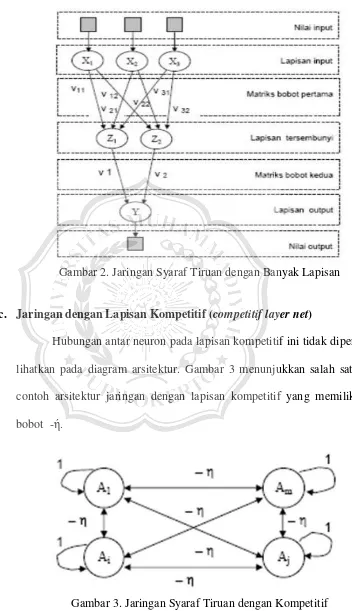
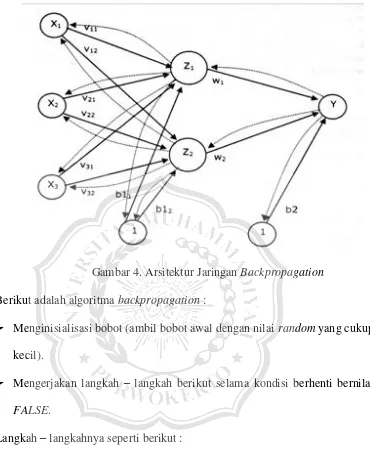
Dokumen terkait
7.1.7 Selepas mendapat pengesahan dari Kumpulan Tuntutan Potongan, disket tuntutan sedia untuk di hantar kepada jabatan ( Prosedur 8 dan fail di e- mail kepada Jabatan Bendahari
digunakan adalah analisis product moment dan koefisien korelasi berganda. Hasil penelitian ini menunjukan : 1) Ada hubungan positif antara tingkat konflik dengan.. produktivitas
Halaman ini berisi menu data basis kasus yang berfungsi mengelola basis kasus dan menu logout untuk keluar dari area pakar. Halaman beranda pakar dapat dilihat pada
Secara umum hasil penelitian menunjukkan ketiga subjek memiliki kecenderungan memandang diri sebagai seorang remaja indigo yang memahami dan menerima keunikan diri yang
Berdasarkan hasil dan pembahasan maka yang dapat diambil bahwa taraf signifikan 5% nilai t tertera bilangan 2,000 oleh bilangan yang diperoleh 6,577 lebih besar dari
Ketiga hal tersebut menjadi kebutuhan ruang yang pada umumnya berada dalam suatu co-working space, namun tidak menutup juga kemungkinan bahwa akan terdapat
Pada tahap ini penulis menyusun semua data yang telah terkumpul secara sistematis dan terperinci sehingga data tersebut mudah di fahami dan temuanya dapat di
Tujuan dari penelitian ini adalah untuk mengetahui penerapan model vee map dalam meningkatkan keterampilan berfikir kreatif siswa yang pada akhirnya dapat meningkatan