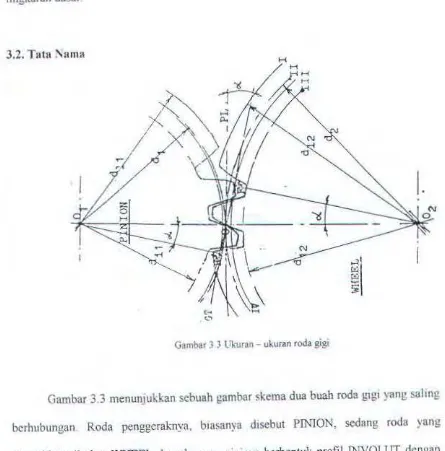
ANALISA KEKUATAN RODA GIGI (S PUR GEAR) DI MESIN JANGKAR DENGAN METODE ELEMEN HINGGA
Teks penuh
Gambar



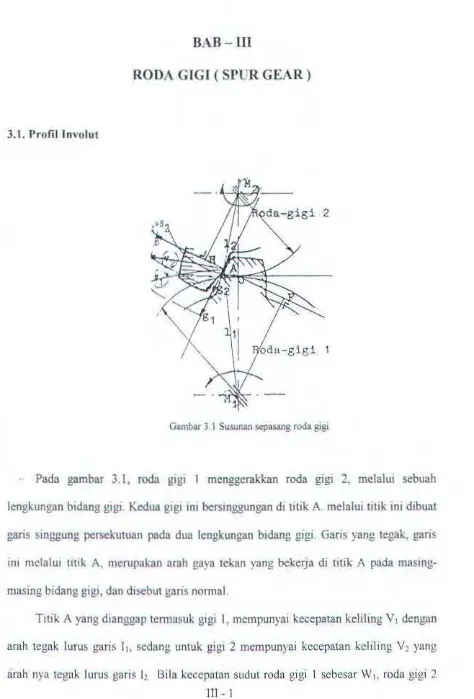
Dokumen terkait
Untuk yang terkasih seluruh anggora keluarga penulis, Bapak, Ibu, dan kakak-kakak, atas segala dukungan dan doa yang tanpa henti, atas kepercayaan dan kekuatan
Struktur yang di buat menggunakan metode ini mengandalkan tidak lebih dari keseimbangan agar tetap tegak. Penggunaan perekat atau cara penyatuan kartu di luar itu tidak di
Mengingat kompleksitas dan luasnya cakupan pengawasan internal BSN, Inspektorat menyusun Rencana Strategis 2020-2024 yang memuat visi, misi, tujuan, sasaran dan strategis,
Nah, dengan meng-unzip file Zip dari folder 02 Data Penuh maka datanya akan sampai dengan Jumat 4 Agustus 2017, sehingga dengan update file DS3-2017- 08.csv maka datanya akan
Keterbatasan data kerugian operasional akan mengurangi akurasi hasil perhitungan beban risiko operasional, untuk itu disarankan agar bank syariah xyz lebih meningkatkan
Selain serat rami dilihat dari rata-rata hasil produksi serat di Indonesia bahwa serat nanas memilki nilai yang paling tinggi [4], dan bila ditinjau dari sifat mekanik yakni
Sedangkan untuk menelusuri hal-hal yang perlu diperhatikan, hasilnya ditampilkan dalam bentuk diagramatis, ditunjang oleh kognisi lingkungan yang dikemukakan oleh