CFA 2019 Level 1 SchweserNotes Book 5
Teks penuh
Gambar



Garis besar
Dokumen terkait
Kelompok kerja Unit Layanan Pengadaan Barang Jasa, telah melaksanakan tahapan Pemberian Penjelasan (Aanwijzing) Dokumen Pengadaan dengan metode tanya jawab secara elektronik
Eksplorasi media untuk mendapatkan media yang sesuai dalam usaha meningkatkan kualitas tanaman lokal yang bernilai ekonomi3. Mempelajari mikroba indigenous untuk
Tujuan penelitian Untuk mengetahui perlindungan hukum terhadap anak sebagai korban tindak pidana kesusilaan dan Untuk mengetahui apa saja kendala yang dihadapi dalam
Hasil pengujian juga dapat diketahui bahwa Independensi berpengaruh secara tidak signifikan terhadap profesionalisme auditor, Dari sumber Mr.X yang tidak mau disebutkan nama
Dari model pertama, diperoleh tiga titik setimbang, yaitu titik setimbang kepunahan , titik setimbang kepunahan predator yang akan eksis dengan syarat tertentu dan bersifat
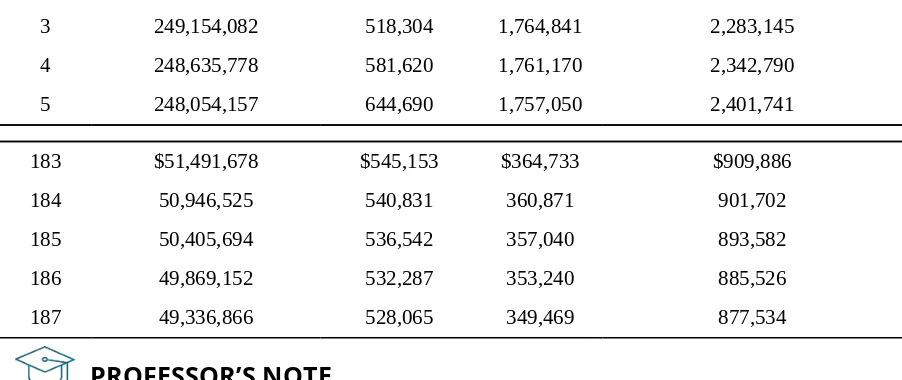
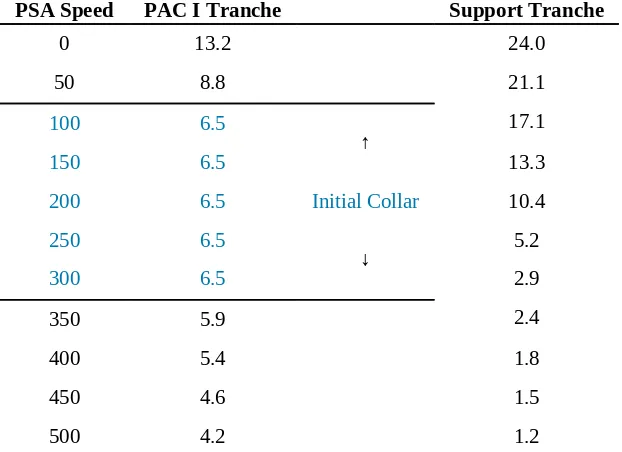
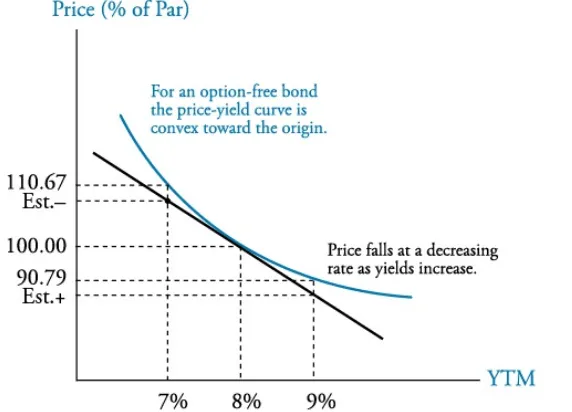
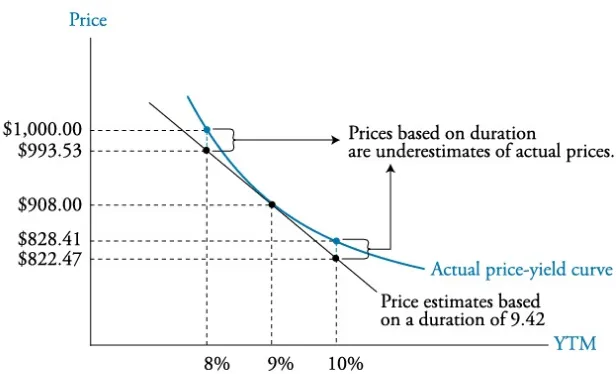
[r]
Beberapa hal penting terkait revaluasi aset yang diatur pada surat keputusan tersebut adalah (a) dalam hal emiten atau perusahaan publik menggunakan model revaluasi untuk aset
memperlakukan Yusuf dengan baik, adalah sebuah perlakuan istimewa, karena sebagai pembesar Mesir tentu dia memiliki ajudan, staf dan pegawai yang mengurusi segala keperluan