The role of material properties for the
Teks penuh
Gambar


Dokumen terkait
Ditulis guna melengkapi sebagian syarat untuk mencapai jenjang Strata Satu (S1). SEKOLAH TINGGI MANAJEMEN INFORMATIKA & KOMPUTER
Usaha untuk memperlancar arus barang dan jasa dari produsen ke konsumen, maka salah satu faktor penting yang tidak boleh diabaikan adalah memilih secara tepat saluran distribusi
Dari ketigapuluh data untuk setiap kombinasi diambil nilai rata-ratanya, sehingga data yang akan diolah tinggal 27 data seperti pada tabel 1.” Fuzzy logic dipergunakan
Puji syukur kehadirat Tuhan yang Maha Kuasa, karena berkat restuNya makalah ini dapat diselesaikan tepat pada waktunya. Budaya sebagai benih identitas suatu bangsa
The response of the Indonesian public to the cases of Prita and Bibit-Chandra and their success sto- ries in controlling the authorities indicate a significant existence of
Selain Taman Nasional Komodo yang mer upakan obyek w isata alam sebagai obyek w isata.. andalan/ utama, Kabupaten Manggar ai Bar at juga memiliki obyek w isata alam lain yang
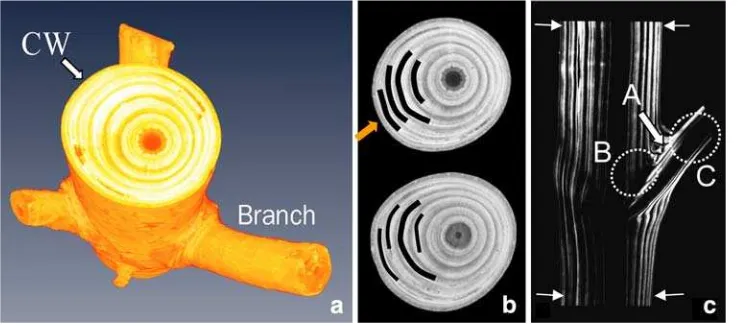
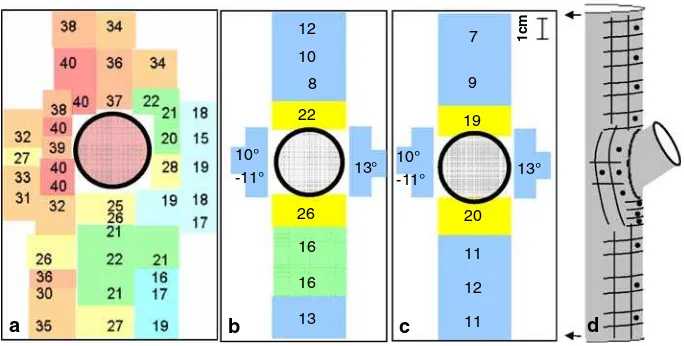
Jabir bebas fibula merupakan salah satu jabir tulang yang sering digunakan untuk mengatasi defek pada daerah wajah, terutama dalam rekonstruksi mandibula8. Jabir ini memiliki
The problem with the single-step random-walk methods is that the sen- timent concepts in the Outside dataset have smaller sentiment values in scale compared to the maximum value