DESIGN OF EXPERIMENT (DOE)
Teks penuh
Gambar
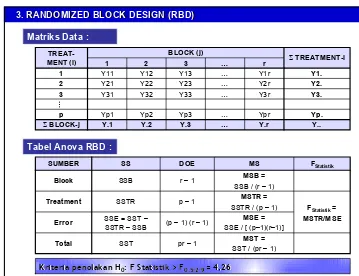
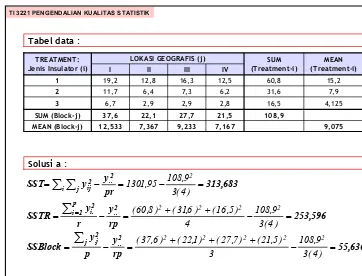
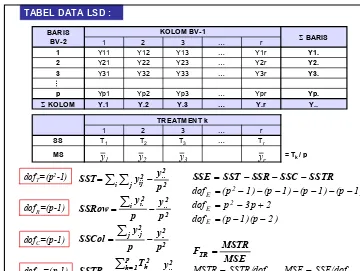
Garis besar
Dokumen terkait
Konsumsi dan kecernaan bahan kering dan bahan organik dalam haylase pakan lengkap ternak sapi Peranakan Ongole.. Relationships between udder and
SENARAI KES PERBICARAAN MAHKAMAH TINGGI DI HADAPAN Y.A DATO’ VAZEER ALAM BIN MYDIN MEERA.. HAKIM MAHKAMAH TINGGI MALAYA, MELAKA
Namun begitu, orang munafik ini tetap menutup kedua-dua telinga mereka dengan jari mereka kerana takut dengan kematian yang akan menimpa mereka. Kenyataan ini membawa maksud
bangunan komplek yang juga memiliki akulturasi budaya antara Islam dan Hindhu. Nilai-nilai historis dalam komplek makam Sunan Kudus banyak mengandung nilai. keislaman. Nilai-nilai
Pada tahapan ikonologi, menghasilkan makna intrinsik/isi, arsitektur dan interior GKIP, merupakan wujud perpaduan dua budaya yang bertemu, yaitu budaya Katolik Roma
Apakah pembelajaran matakuliah CAD pada kelas yang diberi perlakuan dengan penilaian portofolio (penilaian berdasarkan langkah kerja penyelesaian job pada matakuliah
Penelitian ini menggambarkan, bahwa remaja putri dengan obesitas cenderung memiliki karakteristik harga diri rendah, sehingga tidak maksimal dalam mengaktualisasikan
In their thesis, they intended to find out the quality of the English summative test for sixth grade students in