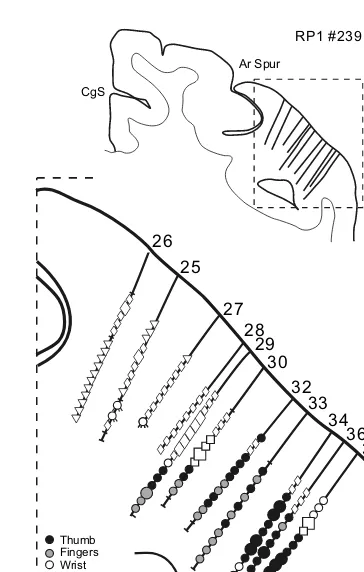
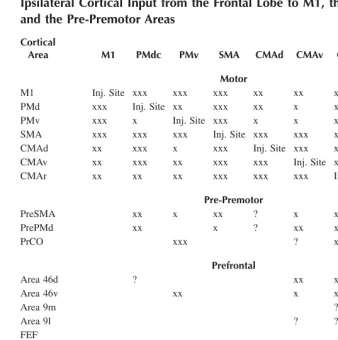
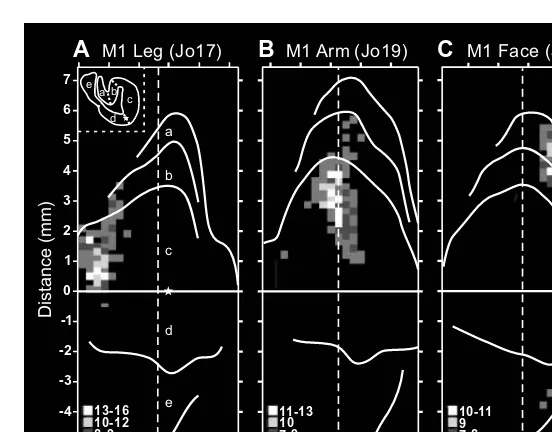
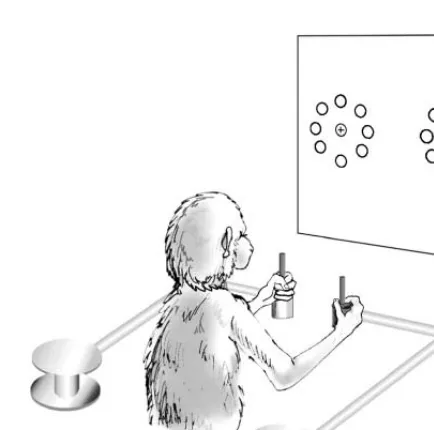
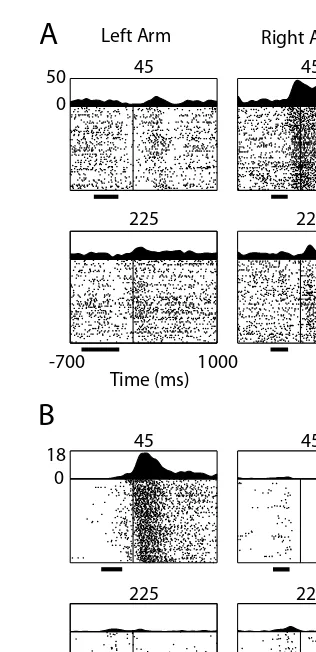
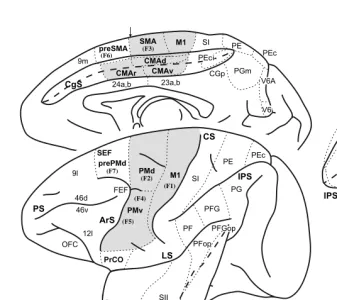
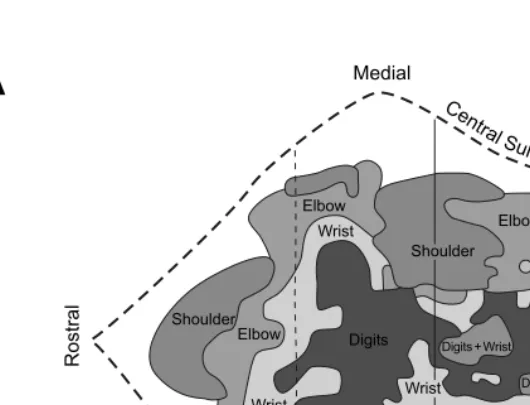
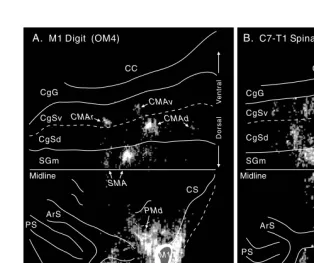
Motor cortex in voluntary movements a distributed system for distributed functions pdf
Teks penuh
Gambar
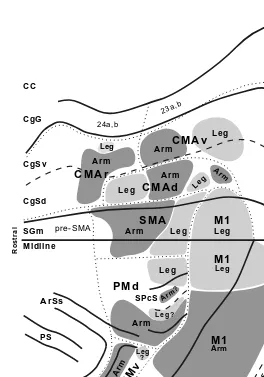
Dokumen terkait
Oleh karena itu, saran yang penulis berikan kepada perusahaan adalah agar perusahaan menjalankan tahapan proses suksesi yang belum dilaksanakan yaitu mengenai
Lingkungan Permukiman Kawasan Kumuh (Paket 2) Kota Banjarmasin, menerbitkan Addendum Dokumen Pengadaan Barang/Jasa untuk Pekerjaan Perbaikan Lingkungan Permukiman Kawasan Kumuh
Sehubungan dengan rujukan tersebut diatas dengan ini diumumkan bahwa Pemenang Penunjukan Langsung pekerjaan tersebut di atas sebagai berikut:.. Nama Perusahaan
Kabupaten Karo. Lembaga keuangan CU Merdeka ini memiliki Unit-Unit yang.. tersebar di berbagai desa di Kecamatan Berastagi Kabupaten Karo dan salah. satunya ada
Dari hasil analisis data diperoleh pengaruh kesiapan siswa pada mata pelajaran produktif terhadap hasil pelaksanaan praktik kerja industri adalah tidak positif
Hasil penelitian menunjukkan 1) jika 10% dari hutan produksi di Kabupaten Biak Nunfor merupakan hutan produksi yang tidak produktif maka diperkirakan terdapat
Dapat digunakan sebagai masukan (bahan pemikiran) keilmuan dan informasi bagi lembaga pendidikan yang dalam hal ini adalah sekolah maupun perorangan, seperti guru pendidikan
pusillus amobil lebih tahan terhadap kondisi lingkungan, menurunnya kadar protein keju tidak hanya disebabkan oleh aktivitas proteolitik dari enzim renin saja tapi juga dari