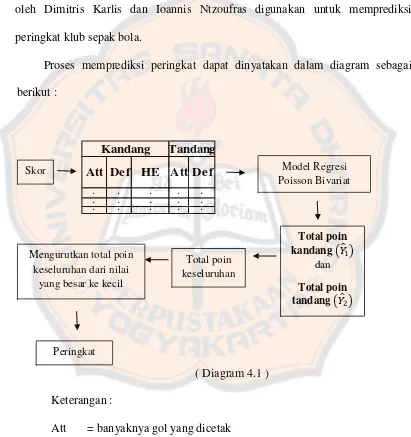
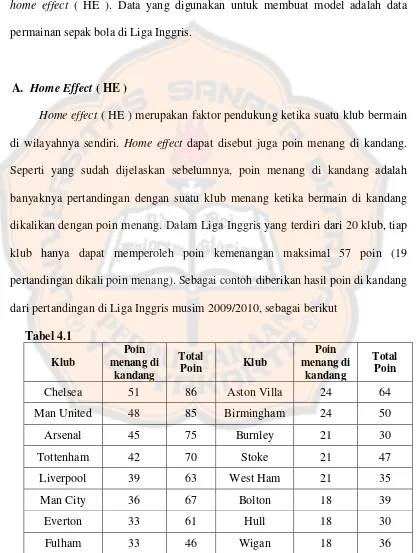
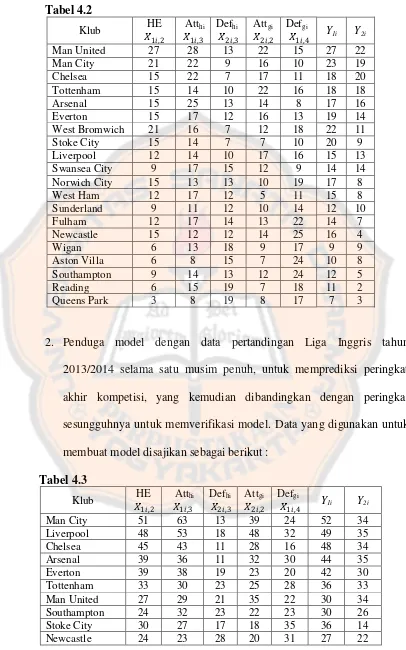
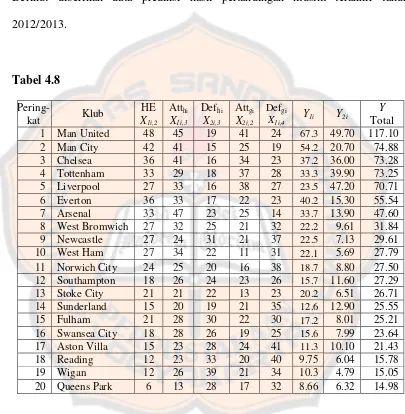
Model regresi poisson bivariat untuk memprediksi peringkat klub sepak bola - USD Repository
Teks penuh
Gambar



Dokumen terkait
faktor : 1) Pernyataan Pemerintah tentang optimisme swasembada beras di.. Tahun 2008; 2) Posisi harga beras dunia yang tidak stabil dan cenderung lebih. tinggi dari HPP; 3)
Visinya yang langsung membawa Indonesia menjadi negara Industri mendapat pertentangan dari berbagai pihak, baik dalam maupun luar negeri yang menghendaki
Hal ini dapat terjadi karena bahasa yang dipergunakan tidak jelas sehingga mempunyai arti lebih dari satu, simbol yang dipergunakan antara si pengirim dan
Penguasaan Pengetahuan, yang merupakan penguasaan pengetahuan program studi sesuai profi lulusan merupakan penguasaan konsep, teori, metode, dan/atau falsafah bidang ilmu
Perencanaan pembelajaran dikembangkan berdasarkan hasil analisis dan refleksi pada tindakan siklus I. Rencana pembelajaran yang dibuat diupayakan agar dapat mengatasi
Pada masa pasca krisis ekonomi terdapat gejolak perbaikan saat periode tahun 1999 dengan sedikit kenaikan yang mencapai laju pertumbuhan 0,79 persen dengan nilai pertumbuhan
Memperhatikan prosedur-prosedur tersebut, dokter seharusnya memperhatikan batasan kerja yang diseskripsikan pada bab ini dalam melaksanakan tindakan persiapan, mengalihkan
Selama melaksanakan PPL 2 di SD Gisikdrono 03 Kecamatan Semarang Barat , Saya mendapatkan banyak pengalaman berharga. Melalui kegiatan praktik mengajar secara