Probability Statistics for Engineers Scientists
Teks penuh
Gambar


Garis besar
Dokumen terkait
This exam can be taken by anyone who missed a regular exam or exams and did not qualify for or could not make it for any reason to the makeup exam given within 3 days after
A large number of practical situations can be described by the repeated per- formance of a random experiment of the following basic nature: a sequence of trials is performed so that
Probabilities associated with binomial experiments are readily obtainable from the formula b ( x ; n, p ) of the binomial distribution or from Table A.1 when n is small. In
Although the method of transforming variables provides an effective way of finding the distribution of a function of several variables, there is an alternative and often
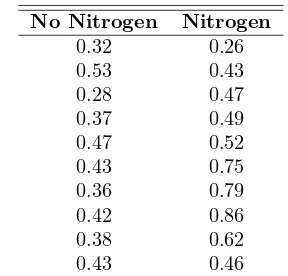
The point and interval estimations of the mean in Sections 9.4 and 9.5 provide good information about the unknown parameter µ of a normal distribution or a nonnormal distribution
For example, if the test is two tailed and α is set at the 0.05 level of significance and the test statistic involves, say, the standard normal distribution, then a z-value is
Example 12.11: Using the techniques of stepwise regression, find an appropriate linear regression model for predicting the length of infants for the data of Table 12.8.. Solution :
If the joint probability density function of continuous random variables Xand Yis fXYx, y, the marginal probability density functionsof Xand Yare 5-16 where Rx denotes the set of all