MODEL PERTUMBUHAN POPULASI TUNGGAL
Teks penuh
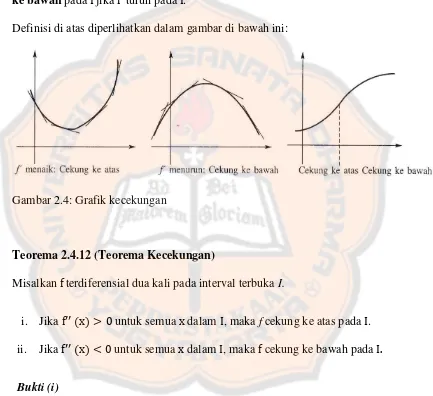
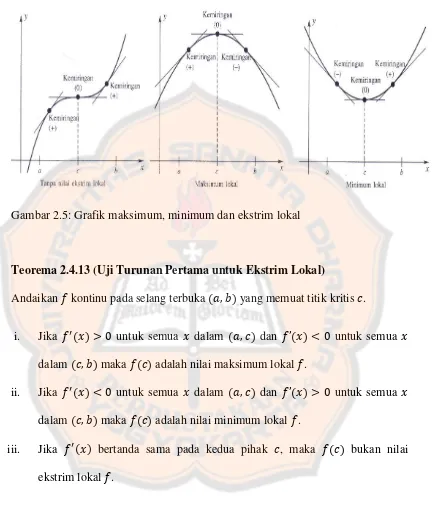
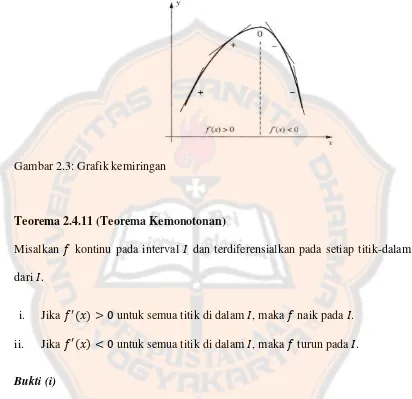
Gambar


Dokumen terkait
adalah lokasi di mana penumpang dapat naik ke dan turun dari angkutan umum dan. lokasi di mana angkutan umum dapat berhenti untuk menaikan dan
Dalam penentuan titik tetap model populasi spesies tunggal pada lingkungan tercemar tanpa waktu tunda, terdapat dua kasus, yaitu kasus pertama merepresentasikan
Pengaruh tingkat pajak dan komposisi pengeluaran pemerintah tipe 1 terhadap output per kapita saat steady state adalah tidak monoton dan berbentuk kurva konkaf,
Berdasarkan hasil analisis data sidik ragam terhadap pertumbuhan jumlah populasi Brachionus plicatilis yang telah dilakukan, didapatkan laju pertumbuhan populasi
Judul Skripsi : Analisis persamaan diferensial model populasi kontinu untuk spesies tunggal Menyatakan bahwa skripsi tersebut adalah karya saya sendiri dan bukan karya orang lain,
Dengan model continous time dapat di tentukan jumlah tumbuhan yang ada dalam beberapa waktu mendatang(Nt), jumlah yang terbentuk dari biji yang dihasilkan oleh tumbuhan yang
Menurut Widodo (2007), pada saat populasi melebihi kapasitas batas, angka kematian cenderung lebih besar dari pada angka kelahiran, sehingga terjadilah penurunan
Data matriks Leslie yang tersedia dalam tugas akhir hanya untuk memprediksi jumlah dan laju pertumbuhan populasi perempuan di Kelurahan Sukaramai I Kecamatan Medan Area