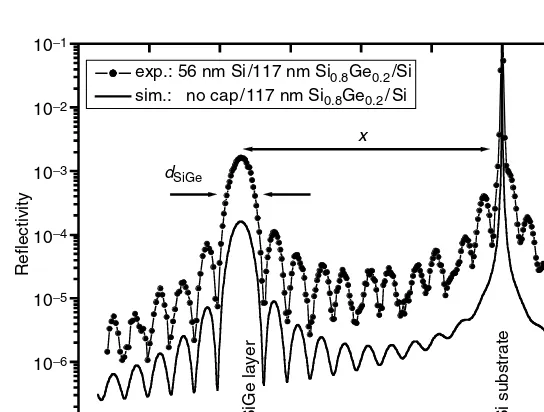
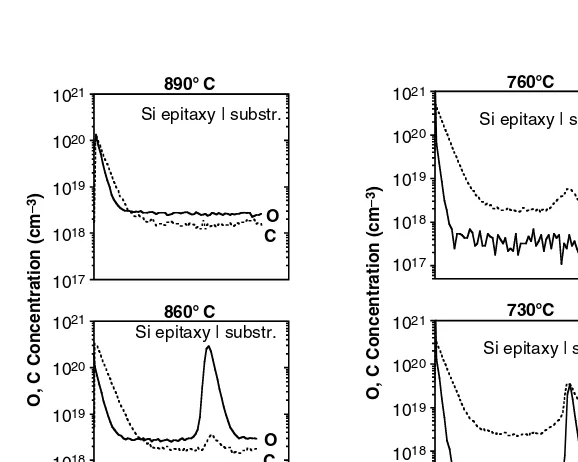
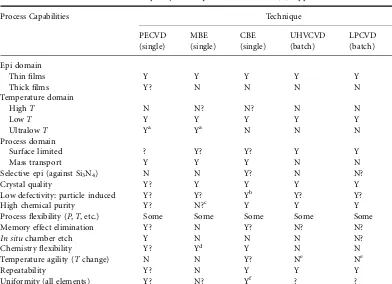
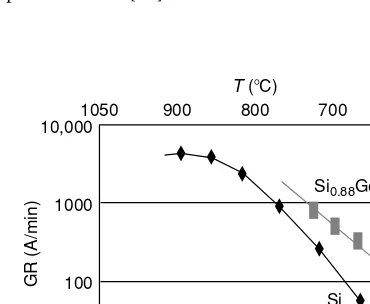
CRC Press SiGe And Si Strained Layer Epitaxy For Silicon Heterostructure Devices Dec 2007 ISBN 1420066854 pdf
Teks penuh
Gambar
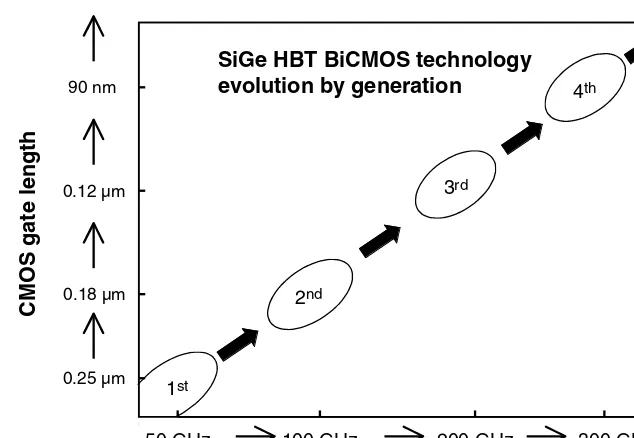
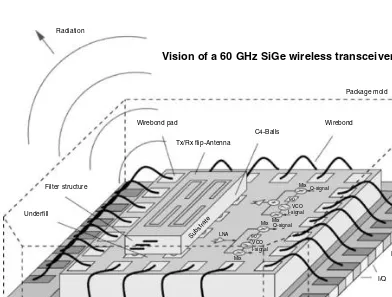


Dokumen terkait
KARAKTERISTIK FISIK, KIMIA DAN FUNGSIONAL TEKNIS PATI SINGKONG RAKYAT DIOKSIDASI MENGGUNAKAN H2O2 DENGAN VARIASI pH DAN LAMA OKSIDASI; Arianto Permadi,
Tutor mengembangkan Peta Konsep berdasarkan hasil kajian materi BMP dan.. Reanalisis Kompetensi
Kejambon pada Dinas Pekerjaan Umum Kota Tegal akan melaksanakan Pemilihan Langsung dengan pascakualifikasi untuk paket pekerjaan konstruksi secara elektronik
Penggunaan Media Film Dokumenter untuk Meningkatkan Kemampuan Menulis Teks Berita (Penelitian Tindakan Kelas terhadap siswa kelas VIII SMP Negeri 16 Bandung). Kemampuan
Sehubungan dengan dilaksanakannya proses evaluasi dokumen penawaran dan dokumen kualifikasi, Kami selaku Panitia Pengadaan Barang dan Jasa APBD-P T. A 2012 Dinas Bina Marga
Pada dasarnya setiap profesi mempunyai problem atau permasalahan yang sudah menjadi tanggung jawab dalam pelaksanaannya, termasuk profesi sebagai jurnalis atau
Tujuan penelitian ini adalah: Untuk Mengetahui Apakah Ada Perbedaan yang Signifikan Antara Kemampuan Menulis Teks Report Siswa Kelas Sebelas SMA 1 Gebog Kudus
The diagnosis of dengue hemorrhagic grade-II with day-3 onset (with hepatic and renal involvement of the liver organ) is established in this patient as a major problem. A