E learning uji beda rata rata
Teks penuh
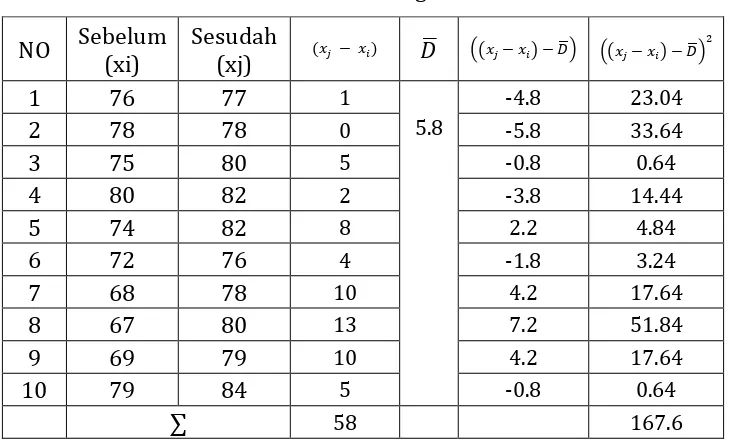
Gambar
Garis besar
Dokumen terkait
Sedangkan untuk nilai Z hitung sebesar -2,226 dengan nilai signifikansi (p) 0,026 artinya p < α, dengan nilai < 0,05 yang berarti ada perbedaan yang bermakna
Oleh karena signifikansi lebih kecil dari 0,05 dengan t hitung -2.953 dan t tabel 1,991 uji dua pihak berarti harga mutlak nilai (-) tidak dipakai artinya (2,953 >
01 lebih kecil atau sama dengan nilai probabilitas sig atau [0.01 ≤ Sig ], maka Ho diterima dan Ha ditolak, artinya tidak signifikan. Jika nilai
Jika bilai signifikansi dari t hitung lebih besar dari nilai α (p > 0,05) maka hipotesis ditolak, berarti tidak ada pengaruh signifikan antara variabel
Nilai signifikansi 0,010 yang berarti bahwa terdapat hubungan yang signifikan antara banyaknya kayuhan terhadap peningkatan prestasi renang gaya dada KU II putera dan
Ini berarti nilai t hitung lebih besar dari t tabel (2,570 > 1,690) maka H 0 ditolak dan H 5 diterima (terdapat pengaruh yang signifikan), yang artinya
Jika nilai signifikansi dibandingkan dengan tingkat signifikan yang digunakan pada penelitian ini ( 0 , 05 ) maka terbukti bahwa nilai signifikansi lebih kecil dari
Dasar pengambilan keputusan Uji T: Jika Nilai sig < 0, 05 atau T hitung > T tabel maka terdapat pengaruh Jika nilai Sig > 0, 05 atau T hitung < T tabel maka tidak terdapat