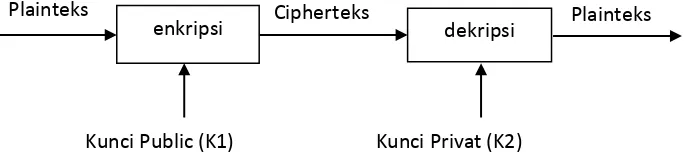
6 BAB 2 TINJAUAN PUSTAKA 2.1 Kriptografi
Teks penuh
Gambar

Garis besar
Dokumen terkait
Kompresi data adalah proses mengubah sebuah aliran data input menjadi aliran data baru yang memiliki ukuran lebih kecil.. Aliran yang dimaksud adalah berupa
Vending machine retailing adalah format ritel bukan toko dimana produk yang dijual disimpan dalam sebuah mesin dan diberikan kepada konsumen apabila mereka
Proses resize pada penelitian ini tidak memerlukan metode khusus, caranya hanya dengan dilakukan perbandingan ukuran antara citra hasil thresholding (pada tahap latih) dan
File format BMP bisa disebut juga bitmap atau format file DIB (untuk perangkat independen bitmap ), adalah sebuah file gambar format yang digunakan untuk menyimpan gambar digital
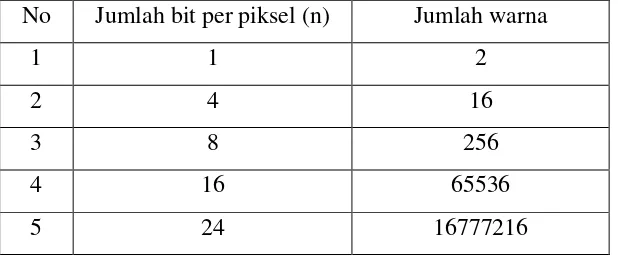
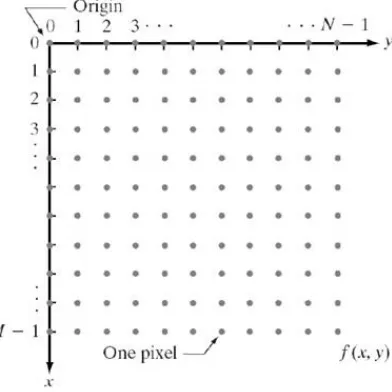
Tahap selanjutnya setelah menjadi citra kontinu yaitu proses sampling, yang merupakan proses untuk menentukan warna pada piksel tertentu pada citra dari sebuah gambar
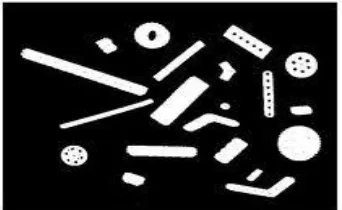
Segmentasi citra (image segmentation) mempunyai arti membagi suatu citra menjadi wilayah-wilayah yang homogen berdasarkan kriteria keserupaan yang tertentu antara tingkat
Pengolahan data yang dapat dilakukan terhadap citra digital antara lain adalah menampilkan bentuk gambar, melakukan perubahan pada gambar, dan mencetak citra
Pada bagian streamvideo ini berisi data yaitu tipe stream yang didefinisikan dengan 4 karakter kode, handler yang menangani kompresi saat file disimpan, kode untuk metode