Fuzzy Logic Controllers Are Universal Approximators
Teks penuh
Gambar
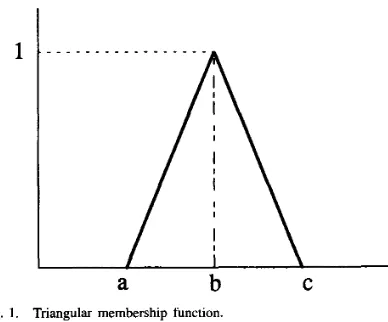

Dokumen terkait
Pengembangan Multimedia untuk Meningkatkan Kualitas Pembelajaran pada Mata Kuliah Media Pembelajaran.. (Tesis) Universitas
[r]
Pendidikan islam adalah penataan individual dan sosial yang dapat menyebabkan seseorang tunduk taat pada islam dan menerapkanya secara sempurna didalam
[r]
o Gejala : setelah terjadi kecelakaan, penderita pingsan atau hanya nyeri kepala sebentar kemudian membaik dengan sendirinya tetapi beberapa jam kemudian timbul gejala-gejala
Demikian pengumuman ini disampaikan untuk diketahui dan atas perhatiannya diucapkan terima kasih.. Makassar, 1 Juli
preservation of historical artefacts; they provide a wide transmissibility of the achieved results, moreover the transition from specialistic knowledge to widespread communication,
Dalam rangka penyelenggaraan pemerintahan daerah sesuai dengan amanat Undang-Undang Dasar Negara Republik Indonesia Tahun 1945, pemerintahan daerah, yang mengatur