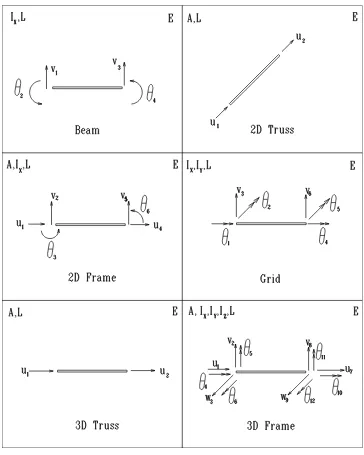
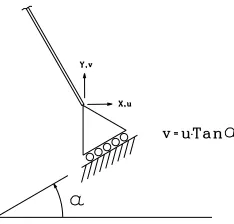
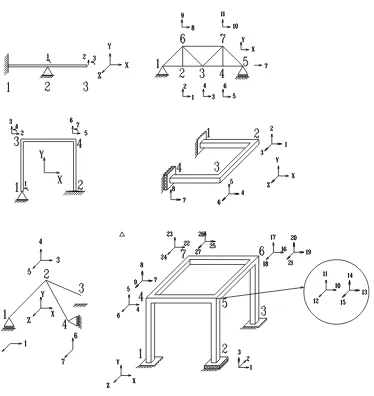
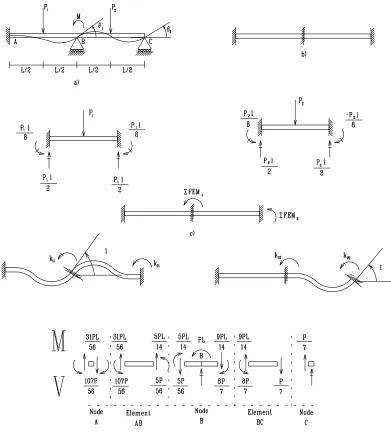
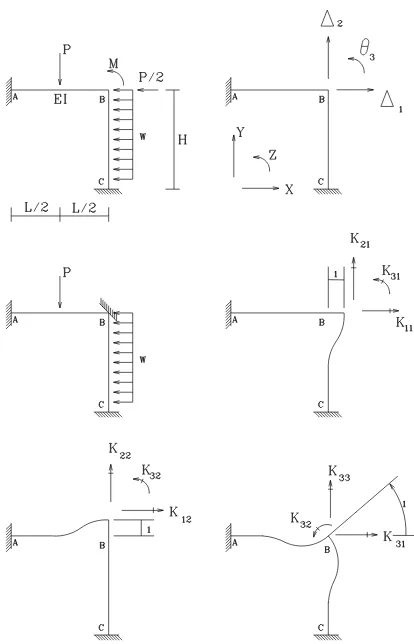
Introduction to Finite Elements CVEN45255525
Teks penuh
Gambar
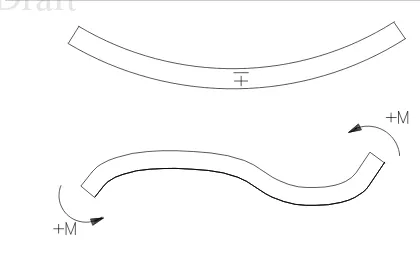
Garis besar
Dokumen terkait
Dengan memenjatkan Puji Syukur Alhamdulillah kehadirat Allah, SWT karena rahmat dan hidayah-Nya, penulis dapat menyelesaikan skripsi yang berjudul : MANFAAT RASIO KEUANGAN
adalah dengan menganalisis data, seluruh data yang telah dikumpulkan dianalisa dengan sedemikian rupa kemudian dihubungkan dengan literatur atau teori yang mempunyai hubungan
Tanpa indexing tabel yang digunakan pada database hanya menggunakan tabel hotspot seperti pada Gambar 17a, sedangkan dengan adanya indexing temporal maka ditambahkan 2 tabel
Those purposes were to describe characteristics of educator, the division of educator task, and educator activities in handling the victims of Papua conflict at PLK Bima Sakti
Besarnya nilai persentase kesehatan tanaman dipengaruhi oleh jumlah tanaman yang dapat tumbuh dengan sehat dari total jumlah tanaman yang hidup dalam plot
[r]
Munawir Sjadzali, Islam and Govermental System: teaching, history, and reflection, (Jakarta: Indonesian-Netherlands Cooperation in Islamic Studies [INIS],
Untuk sumber data penulis menggunakan 2 langkah yaitu mengumpulkan beberapa dokumen tentang daftar rekapitulasi Gaji pegawai, Rekapitulasi perhitungan uang makan