penalaran matematis siswa
Teks penuh
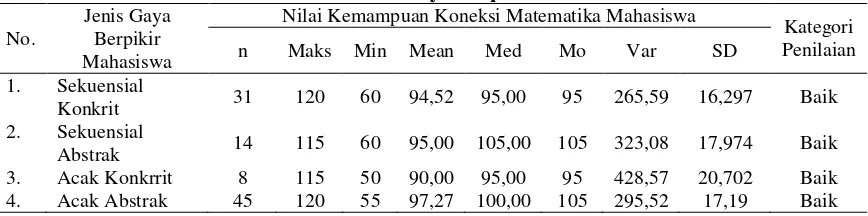
Gambar


Garis besar
Dokumen terkait
Bagi meningkatkan pencapaian subjek Sains dan Matematik agar setanding dengan negara lain, setiap pelaksanaan program pendidikan negara perlu diperhalus.. Selain
Dengan terwujudnya kebiasaan makan yang baru tersebut, ketergantungan terhadap salah satu komoditas pangan dapat direduksi.Di era desentralisasi ini, untuk mengaplikasikan
manfaat hasil belajar Fashion Style and Trend Research , dan prinsip dasar Fashion Style and Trend Resea rch sebagai kesiapan menjadi Fashion Foreca ster oleh mahasiswa
Beberapa penelitian sebelumnya menunjukkan bahwa kecemasan matematika memiliki keterkaitan dengan hasil belajar yang diperoleh siswa. Penelitian lain mengenai
Teknik pengumpulan data yang digunakan dalam penelitian ini adalah..
ANALISIS PASCA PENGAMPUNAN PAJAK UNTUK MENCAPAI TARGET PENERIMAAN PAJAK TAHUN 2017.. Manajemen
14 Sedangkan hasil penelitian mengenai “Pengaruh Inflasi, BI RATE, PDB dan Nilai Tukar Rupiah Terhadap Simpanan Mudharabah Pada Bank Syaria h di Indonesia “
Karena amarah ketiga dewa itu sudah tidak dapat ditahan lagi, tiba-tiba dari mulut mereka keluar lidah api yang sangat besar.. Lama kelamaan, lidah itu berubah