Java Data Analysis Ebook free download pdf pdf
Teks penuh
Gambar


Garis besar
Dokumen terkait
The acquisition of Freebase by Google and Powerset by Microsoft are the first indicators that large enterprises will not only use the Linked Data paradigm for
But because the pioneers of unikernel technology are also established software engineers, they made sure that development and debugging of unikernels is a very reasonable
Although some of the tools in the Hadoop stack offer data governance capabilities, organizations need more advanced data governance capabilities to ensure that business users and
Cloud computing provides the IT leadership a cost-effective and predictable solution for reliably meeting their large data management needs.. There are many vendors offering
static : The static keyword is used to declare member variables and methods as belonging to the class rather than the instances of the class. Members that are marked as static
Going beyond the typical points of data collection, and diving deeper into things like trending products and location-based preferences, these companies are using sales data to
Be careful with capturing groups inside a lookahead or lookbehind atomic group Lookbehind limitations in Java regular
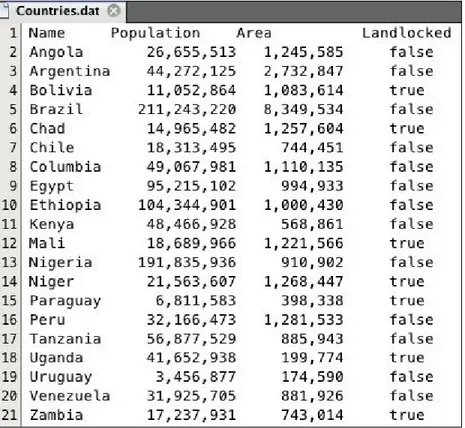
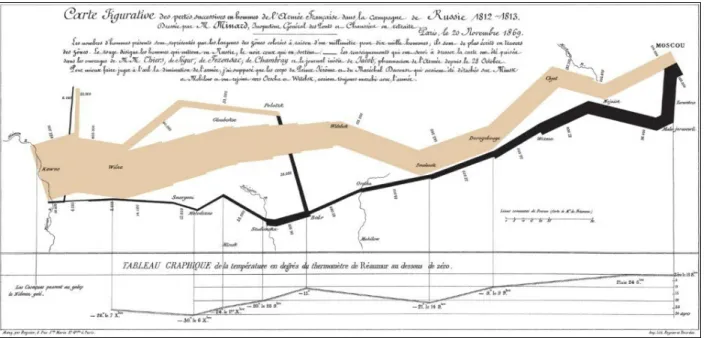
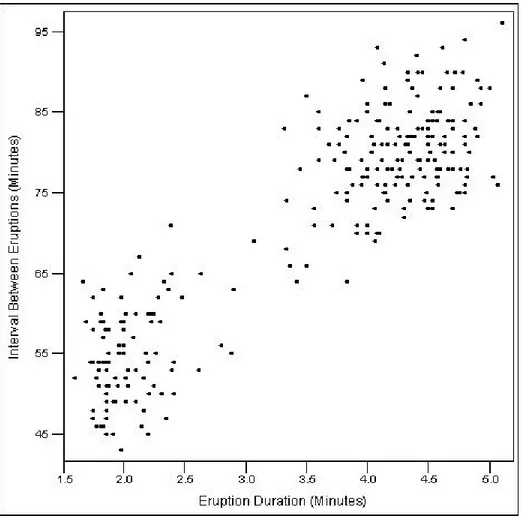
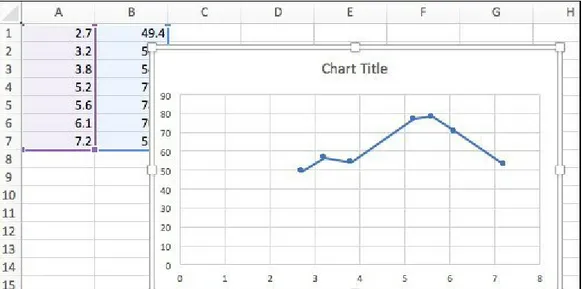
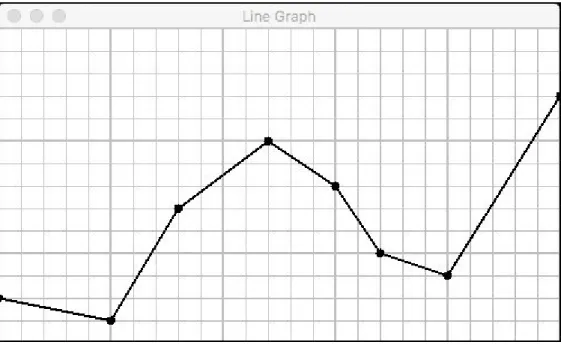
Data visualization is an important part of our data analysis process because it is a fast and easy way to do an exploratory data analysis through summarizing their