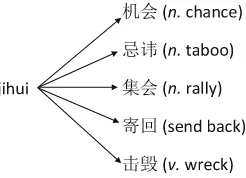
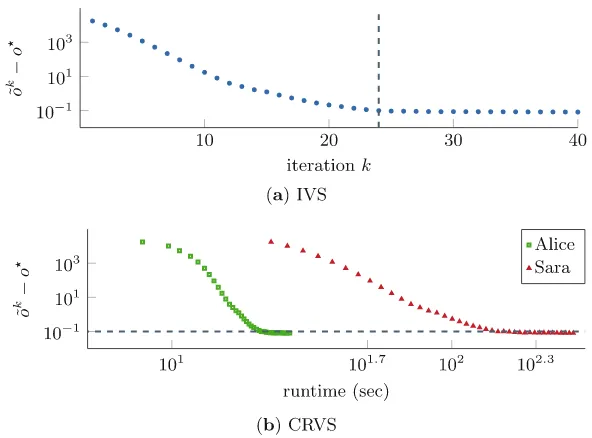
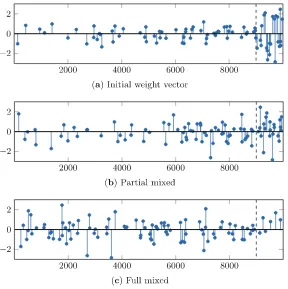
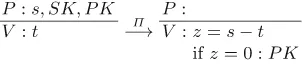Computer Security ESORICS 2015 Part II pdf pdf
Teks penuh
Gambar
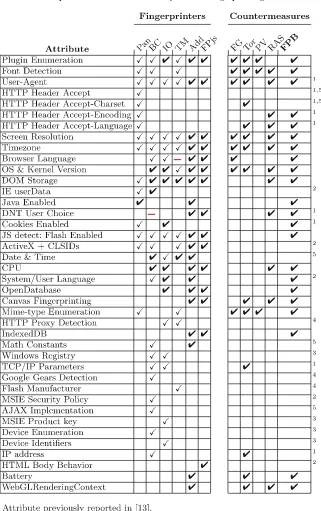


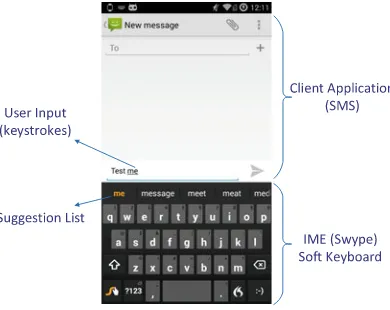
Garis besar
Dokumen terkait
Jika unit-unit kristal tersusun secara homogen membentuk padatan maka padatan yang terbentuk memiliki bangun yang sama dengan bangun unit kristal yang membentuknya namun dengan
Jika dibandingkan antara jumlah pos hujan usulan analisis metode Kagan dengan kondisi yang ada saat ini, dapat dikatakan secara kuantitas pos hujan dan pos
For Malaysia, the estimation result indicated that we reject the null hypothesis of GDP does not Granger cause DX and conclude that there is exists uni-directional
Sebuah Tesis yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan (M.Pd.) pada Program Studi PendidikanSeni. © Didi Sukyadi 2014 Universitas
Frekuensi penyajian ransum dilakukan untuk meningkatkan konsumsi ransum dan menyediakan ransum dalam keadaan kontinyu agar ayam dapat makan kapan saja dan
Dalam satu golongan, dari atas ke bawah, energi ionisasi pertama cenderung semakin kecil, sebagaimana jarak dari inti ke elektron terluar bertambah sehingga tarikan elektron
Sesuai dengan arahan pada PP Nomor 26 Tahun 2008 tentang Rencana Tata Ruang Wilayah Nasional, Pusat Kegiatan Strategis Nasional atau PKSN adalah kawasan perkotaan yang ditetapkan
Dinamika sosial politik Indonesia yang juga berdampak pada perubahan kurikulum merupakan suatu bentuk penyempurnaan dalam bidang pendidikan untuk meningkatan