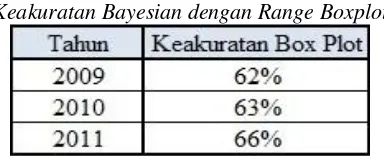
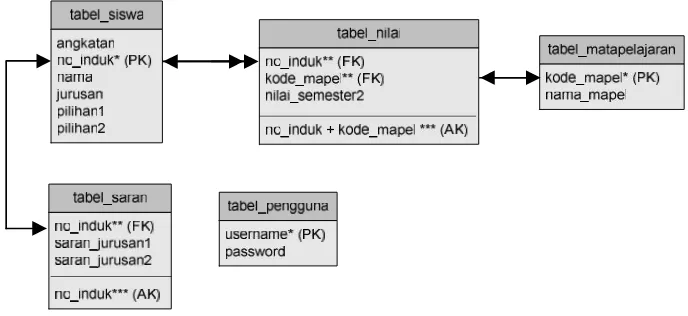
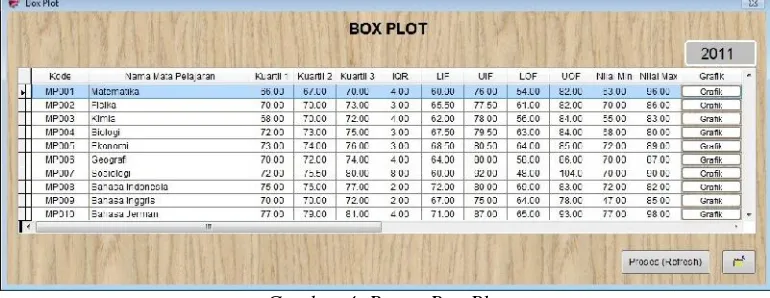
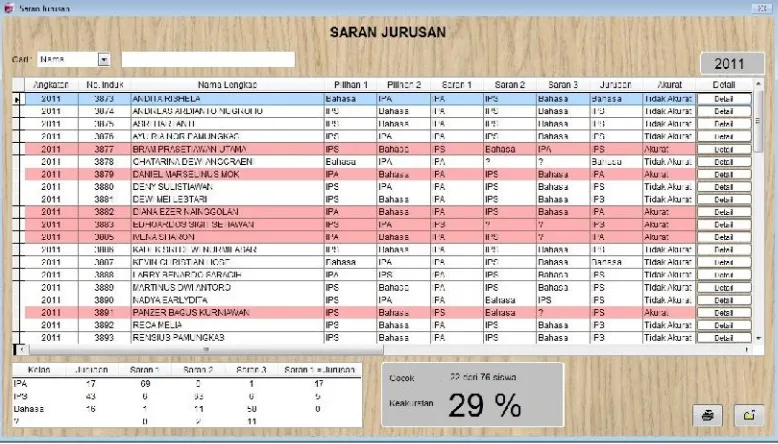
IMPLEMENTASI METODE BAYESIAN DALAM PENJURUSAN DI SMA BRUDERAN PURWOREJO STUDI KASUS: SMA BRUDERAN PURWOREJO
Teks penuh
Gambar

Dokumen terkait
Dari hasil analisis Rank Spearman , dapat diketahui bahwa faktor sosial ekonomi yang memiliki hubungan nyata dengan tingkat adopsi inovasi petani dalam program PAT Padi Sawah
Pada perancangan panti asuhan anak ini, maka material dinding menggunakan material finishing yang aman, ramah lingkungan, dan mudah dibersihkan.. Untuk pemilihan
Guru memberikan kesempatan pada peserta didik untuk mengidentifikasi sebanyak mungkin pertanyaan yang berkaitan dengan gambar yang disajikan dan akan dijawab melalui
dalam Pasal 6 ayat (2) tidak diketahui atau lebih rendah dari NJOP yang digunakan dalam pengenaan Pajak Bumi dan Bangunan pada tahun terjadinya perolehan, besaran pokok Bea
Gangguan yang timbul pada akhir kehamilan atau persalinan hampir selalu disertai anoksia/hipoksia janin dan berakhir dengan asfiksia neonatus dan bayi mendapat perawatan
Hal tersebut menunjukkan bahwa usia responden peternak sebagian besar pada usia produktif (15-64 tahun), yang berarti bahwa dengan usia produktif sebagian besar
3.2 Pelaksana an Bea Perolehan Hak atas Tanah dan Bangunan di Kabupaten Daerah Tingkat II Madiun dalam Meningkatkan Penerimaan Pajak
Data sekunder tersebut berupa perturan perundang-undangan dan literatur- literatur yang terkait, yang kemudian dihubungkan dengan fakta-fakta yang ada dari permasalah