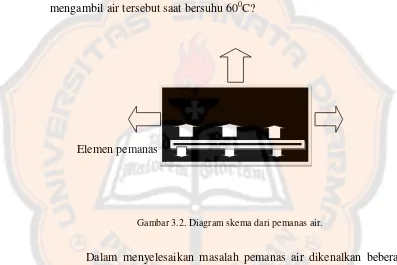
Pemodelan matematika mengenai masalah konduksi panas - USD Repository
Teks penuh
Gambar


Dokumen terkait
Menyatakan bahwa skripsi saya berjudul “ PENINGKATAN KETERAMPILAN MEMECAHKAN MASALAH MATEMATIKA MELALUI PENERAPAN MODEL PEMBELAJARAN KOOPERATIF TIPE THINK TALK
Hasil penelitian menunjukkan bahwa (1) Langkah-langkah pembelajaran yang secara konsisten dapat dilaksanakan dalam pembelajaran matematika dengan model pembelajaran berbasis
Penelitian ini membahas tentang pengaruh model pembelajaran kooperatif tipe numbered heads together (NHT) berbasis masalah kontekstual terhadap hasil belajar matematika siswa
Slaipsl dengan judul "Kemampuan Pemecahan Masalah Matematika Berbenuk Soat Cerita Berdasarkan Model Polya Materi Pokok Sistem Persamaan Linear Dua Variabel (SPLDV) pada
Tiga buah tugas yang berkaitan dengan masalah fungsi linear telah diberikan kepada subyek penelitian untuk diselesaikan menggunakan program geogebra, mereka bebas
Peningkatan Hasil Belajar dan Keterampilan Pemecahan Masalah Matematika Siswa Kelas IV Melalui Model Problem Based Learning (PBL) Berbantuan Kotak Hitam Putih SD