Decision and Game Theory for Security pdf pdf
Teks penuh
Gambar


Garis besar
Dokumen terkait
Sebuah Tesis yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan (M.Pd) pada Fakultas Sekolah Pascasarjana. © Emilia Yesi Giyok 2016
Berdasarkan hasil koreksi aritmatik dan evaluasi penawaran terhadap 10 (sepuluh) peserta yang memasukkan penawaran, Unit Layanan Pengadaan (ULP) Kelompok Kerja Pengadaan
1). Bagaimana bentuk fungsi kuadrat yang diperoleh dari masalah 3 dan 4 dengan peubah bebasnya anggota himpunan bilangan real ? Berapakah nilai peubah bebas dari
checkbox 1 1.Aplikasi Checkbox (memilih kotak yang sesuai dengan kebutuhan, kemudian klik kotak yang sesuai) Keterangan gambar:.. radio 1 1.Aplikasi radio (memilih
Namun yang dimaksudkan dalam kajian ini adalah seyogianya para pihak menuangkan dan mengimplementasikan asas proporsionalitas ini ke dalam klausul-klausul kontrak yang mereka
Penelitian ini bertujuan untuk mengetahui hubungan yang positif antara adversity quotient dan loyalitas kerja pada Pegawai Negeri Sipil di Dinas Perhubungan
Perancangan dan pembuatan firmware untuk mikrokontroler yang berfungsi sebagai pengendali dari input data (berupa tombol input ) dan pengendali rangkaian
Perumahan nasional merupakan suatu pemukiman yang perencanaanya diangun oleh negara dimana dengan adanya pemukiman tersebut dapat berguna membantu masyarakat

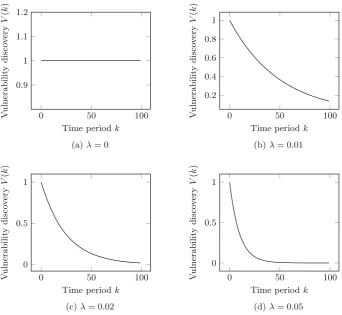
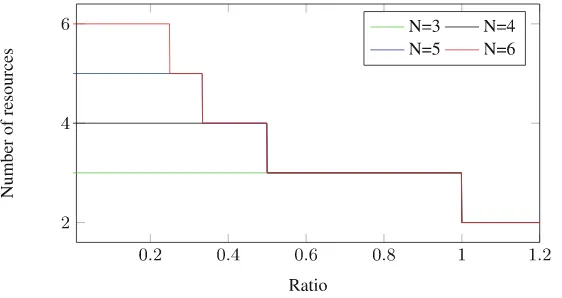
![Fig. 3. The effects of varying resource constraints and r1, where w = [2 2 2 2 2],CD = CA = [1 1 1 1 1], B = 0.5, r = [5 4 3 2 1] in (a), r = [r1 1 1 1 1] and M = 0.3in (b).](https://thumb-ap.123doks.com/thumbv2/123dok/3934928.1878348/120.439.66.362.63.293/fig-eects-varying-resource-constraints-cd-ca-m.webp)