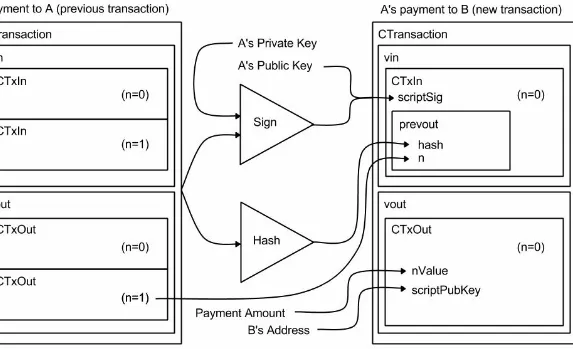
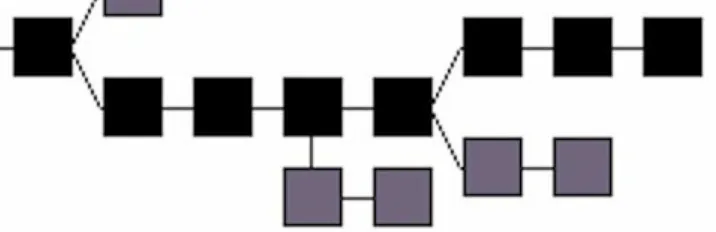
Bitcoin Internals A thorough explanation of Bitcoin and how it works from a technical perspective pdf pdf
Teks penuh
Gambar
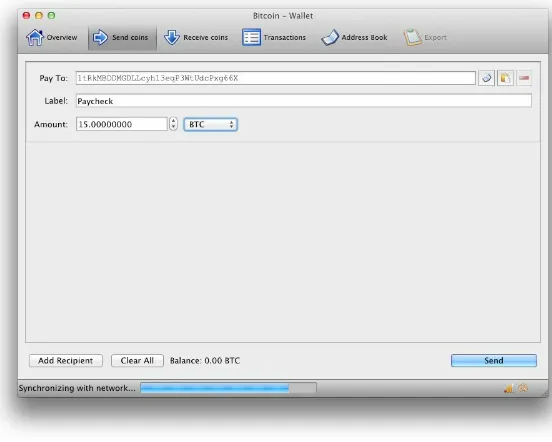
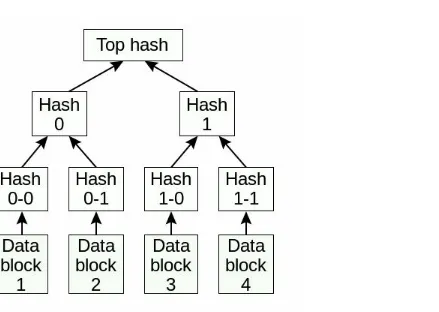
Dokumen terkait
Adapun hal yang menjadi alasan untuk melakukan penelitian efektivitas pendekatan cognitive behavioral therapy dengan setting kelompok untuk meningkatkan motivasi
home pain. So that later hospital side and or individual owning this data will feel getting a disadvantage. To anticipate from undesirable things like forgery of data,
The weakest and strongest battery cell position changes were performed that is from cell 3 to cell 4 and vice versa then the experiment for 9 charging and discharging
Along with the conclusions, propose the following suggestions: (1) the school management should monitor the performance of teachers through classroom
Perilaku kepala sekolah yang mampu memprakarsai pemikiran baru dalam proses interaksi dilingkungan sekolah dengan melakukan tujuan, prosedur, input, proses dan
Hasil uji reliabilitas dengan internal consitency alat ukur dalam mengidentifikasi potensi anak cerdas istimewa dan berbakat istimewa yang dilakukan pada uji terbatas
Dari penelitian ini dapat disimpulkan bahwa penelitian ini berhasil memanfaatkan limbah ampas tebu dan kulit durian menjadi kandidat bahan bakar padat berupa briket hibrida
[r]