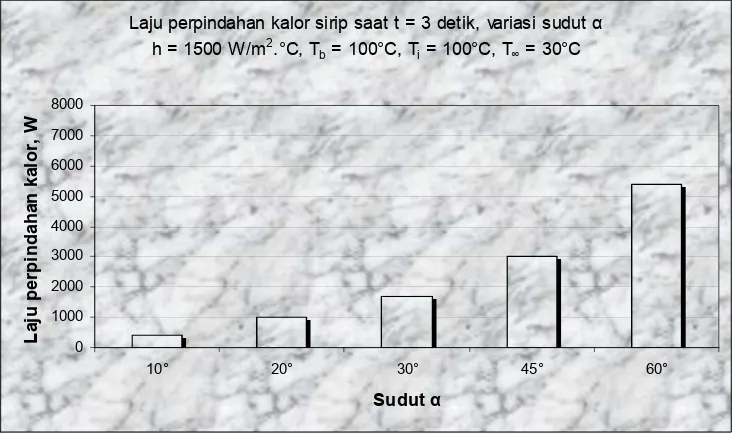
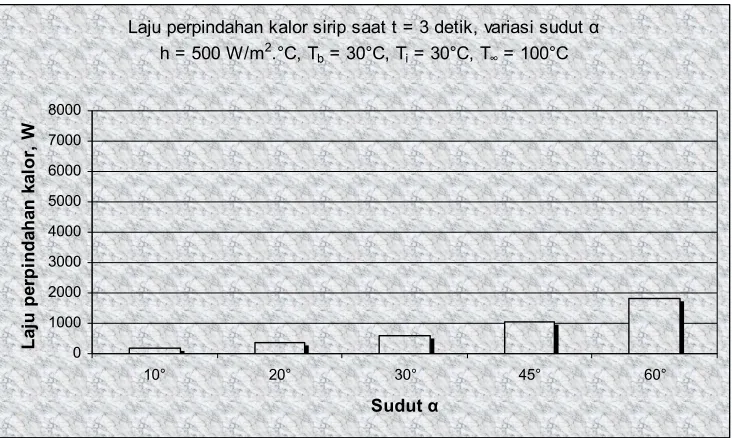
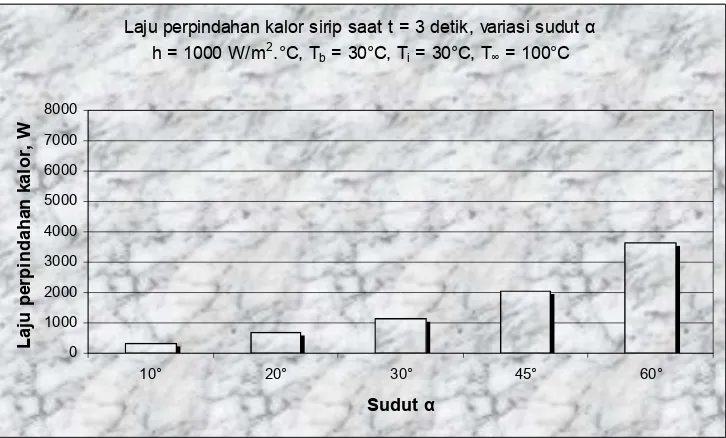
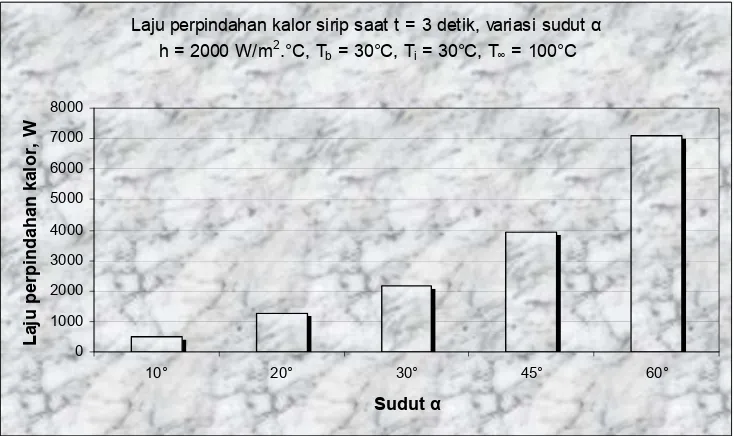
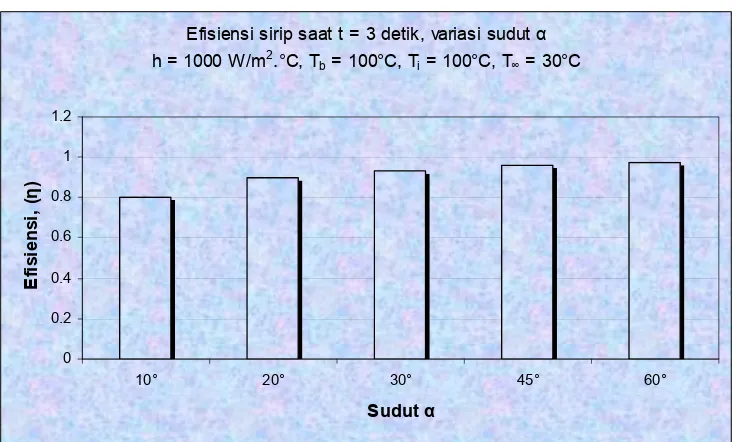
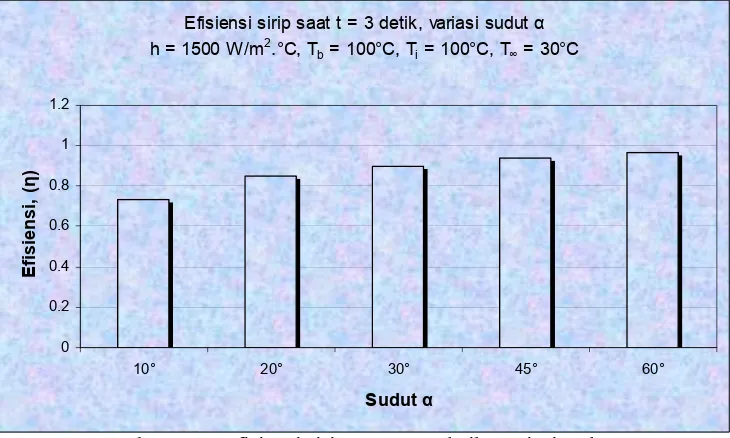
PERPINDAHAN KALOR PADA SIRIP LIMAS SEGIENAM KEADAAN TAK TUNAK k = k (T)
Teks penuh
Gambar

Dokumen terkait
SKRIPSI SISTEM DASHBOARD UNTUK … AUFA AKMAL R Layout dashboard standar 7 pada gambar 4.40 terdiri dari 3 komponen, yaitu tabel nilai deskripsi elemen penilaian, dashboard
Setelah dilakukan penelitian mengenai Pengaruh Mobilisasi Dini terhadap Keberhasilan Penyembuhan Luka pada Pasien Pasca Operasi di Bangsal Arofah dan Marwah RS PKU
Masalah yang mungkin terjadi dengan mengatur bahwa setiap proses hanya dapat memiliki satu proses adalah bahwa tidak semua proses hanya membutuhkan satu
Berdasarkan hal tersebut maka untuk menciptakan nilai tambah dari produksi minyak sawit perusahaan perkebunan, sudah saatnya membangun industri hilir minyak sawit yang
Karena adanya multi-path channel, metode time-reversal memiliki kelebihan dalam mendeteksi sinyal seperti yang telah disebutkan pada gambar (4.1) dan (4.2)
Penetapan harga dasar gabah dan harga atap beras di tingkat konsumen lebih rendah daripada harga keseimbangan di pasar dengan tidak ada subsidi kepada produsen maka
Polisi Pamong Praja adalah aparatur pemerintah daerah yang melaksanakan tugas Bupati dalam memelihara ketentraman dan ketertiban umum serta menegakkan Peraturan
BB 2757 MI yang dikemudikan oleh korban Marmeilin Sipahutar (meninggal dunia) dengan cara terdakwa keluar dari kantor CU Pinangsori lalu pergi dengan mengendarai