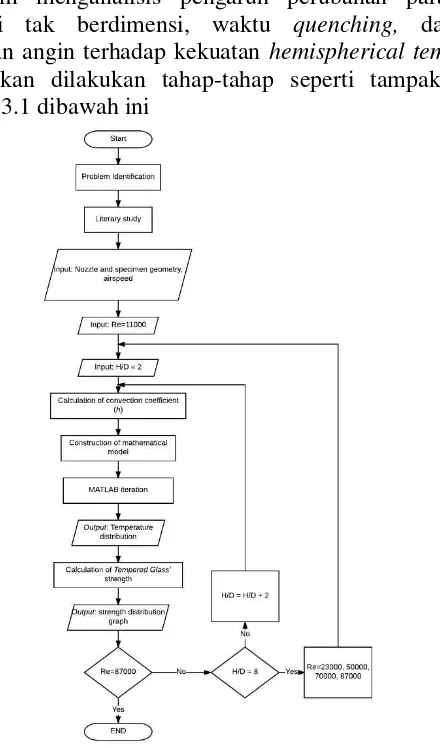
DISTANCE RATIO DAN BILANGAN REYNOLDS TERHADAP KEKUATAN DAN WAKTU QUENCH
Teks penuh
Gambar

![Gambar 2.1 Profil distribusi tegangan pada penampang tempered glass[3]](https://thumb-ap.123doks.com/thumbv2/123dok/1783396.2095572/23.420.131.321.306.487/gambar-profil-distribusi-tegangan-pada-penampang-tempered-glass.webp)
![Gambar 2.2 Skema spesimen yang digunakan untuk mencari ukuran pecahan dengan analisis strain energy [7]](https://thumb-ap.123doks.com/thumbv2/123dok/1783396.2095572/25.420.143.290.75.221/gambar-skema-spesimen-digunakan-mencari-ukuran-pecahan-analisis.webp)
![Gambar 2.4 Grafik temperatur permukaan dan interior kaca tebal 4mm terhadap waktu pada proses pemanasan dan quenching[4]](https://thumb-ap.123doks.com/thumbv2/123dok/1783396.2095572/27.420.68.364.228.484/gambar-grafik-temperatur-permukaan-interior-terhadap-pemanasan-quenching.webp)
Dokumen terkait
Setelah 15 hari diinduksi, tikus diukur tekanan darahnya terlebih dahulu dan yang digunakan adalah tekanan darah diatas 150 mmHg (7). 3) Tikus putih jantan dibagi secara random
terhadap kinerja perusahaan Penelitian ini menentukan tingkat kinerja perusahaan pada Balai Besar Pengembangan Penangkapan Ikan Semarang dengan menggunakan empat perspektif
Aset perusahaan menunjukkan keputusan investasi pada masa lalu, sedangkan klaim perusahaan menunjukan sumber dana tersebut atau keputusan pendanaan pada masa lalu, dana
Peran serikat-serikat pekerja ini khususnya AFL dan CIO menjadi sangat terlihat pada masa New Deal (1933-1939), karena pada masa ini para pekerja Amerika
(1) Dalam melaksanakan tugasnya Sekretaris Daerah, para Asisten Sekretaris Daerah, para Kepala Bagian, para Kepala Sub Bagian dan Kelompok Jabatan Fungsional wajib
•• Memberikan pendekatan yang sistematis bagi pengembangan teknologi yang Memberikan pendekatan yang sistematis bagi pengembangan teknologi yang berorientasi
Visi Panin Life adalah menjadi perusahaan jasa keuangan ritel terkemuka di Indonesia, yang mampu memberikan solusi inovatif yang dapat memuaskan kebutuhan nasabah baik untuk

![Gambar 2.9 Tampak atas untuk (a) single round jet, (b) square-in-line array of round jets, (c) equilaterally staggered array of round jets, (d) single slot jet, dan (e) array of slot jets[9]](https://thumb-ap.123doks.com/thumbv2/123dok/1783396.2095572/33.420.78.356.220.472/gambar-tampak-untuk-single-square-equilaterally-staggered-single.webp)
![Gambar 2.10 Degree of temper sebagai fungsi dari heat transfer coefficient dan temperatur awal quenching pada flat tempered glass dengan ketebalan 0.61 cm[5]](https://thumb-ap.123doks.com/thumbv2/123dok/1783396.2095572/35.420.120.314.228.463/gambar-degree-transfer-coefficient-temperatur-quenching-tempered-ketebalan.webp)
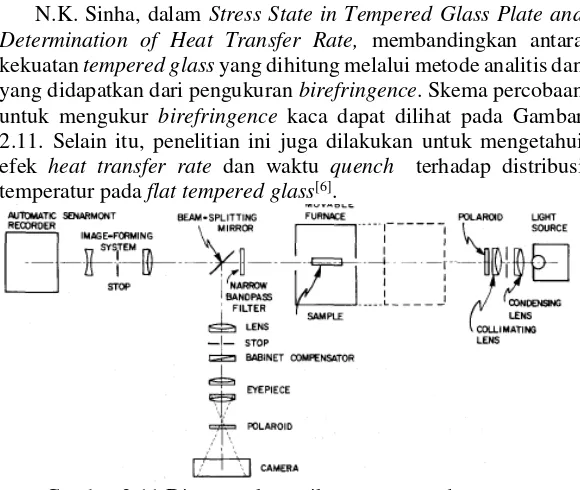
![Gambar 2.13 Efek variasi terhadap perbedaan temperatur heat transfer rate dan waktu quench midplane dengan temperatur rata-rata[6]](https://thumb-ap.123doks.com/thumbv2/123dok/1783396.2095572/38.420.130.273.73.280/gambar-variasi-perbedaan-temperatur-transfer-quench-midplane-temperatur.webp)