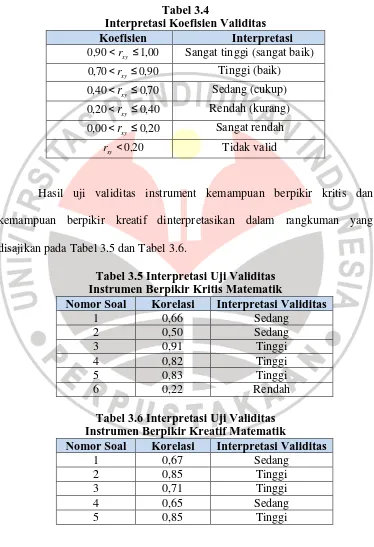
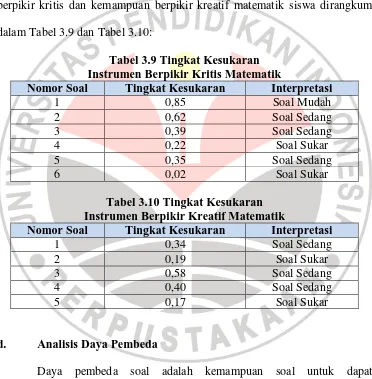
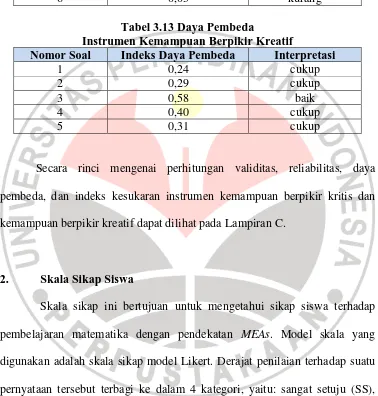
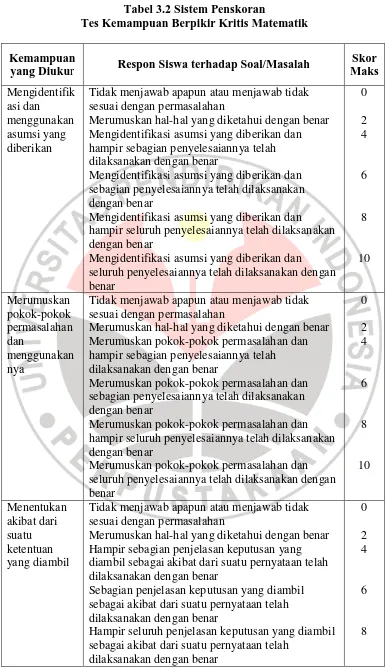
Meningkatkan Kemampuan Berpikir Kritis dan Kreatif Matematik dengan Pendekatan Model Eliciting Activities (MEAs) pada Siswa SMA.
Teks penuh
Gambar

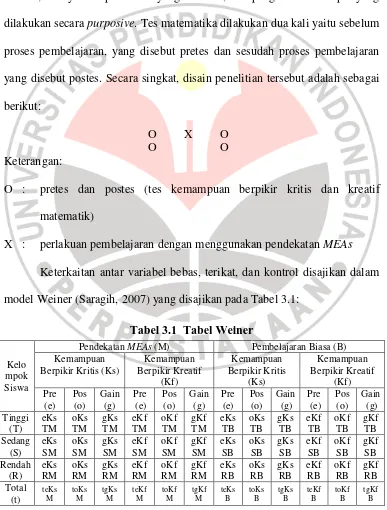

Dokumen terkait
ApaI and FokI polymorphisms of VDR gene do not appear to be responsible for host susceptibility to pulmonary tuberculosis in the Indonesian Batak ethnic population but
Berdasarkan Peraturan Menteri Dalam Negeri Nomor 54 Tahun 2007 tentang Pedoman Pembentukan Kelompok Kerja Operasional Pos Pelayanan Terpadu (Pokjanal Posyandu) dan
Polrestabes Semarang yang turut memberikan perlindungan hukum kepada anak korban kekerasan seksual. Data yang diperoleh dari wawancara tersebut sangat berguna untuk
[r]
In order to make the current generated by the source relatively immune to the disturbance of power source, the voltage to generate the current is fed from the
Dengan demikian, berdasarkan pendapat para ahli di atas dapat simpulkan bahwa sampel merupakan bentuk kecil yang mewakili suatu populasi yang sifatnya harus benar-benar representatif
Berdasarkan Peraturan Presiden Nomor 70 Tahun 2012 tentang Perubahan Kedua atas Peraturan Presiden Nomor 54 Tahun 2010 tentang Pengadaan Barang/Jasa Pemerintah Bagian
Rumusan kebijakan secara tepat yang dimaksud adalah rumusan bauran kebijakan yang sinergis/selaras, dalam arti tidak saling bertentangan/menegasikan satu sama lain