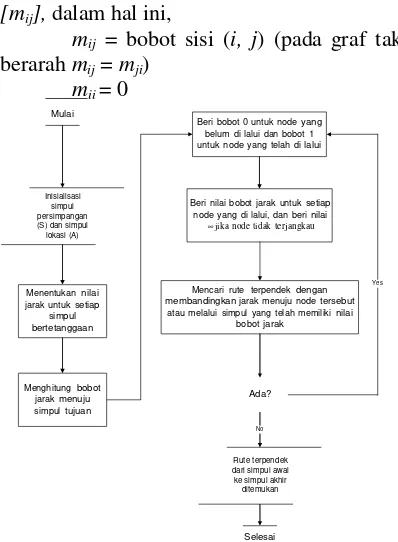
PENENTUAN RUTE TERPENDEK PENDIS TRIBUSIAN
Teks penuh
Gambar


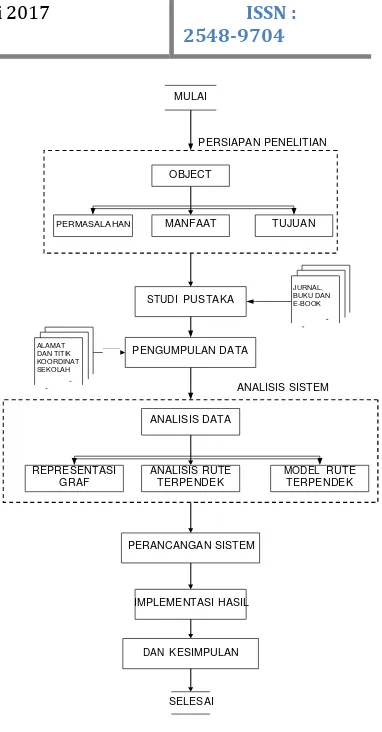

Garis besar
Dokumen terkait
[r]
However, they do in principle include key ingredients that can be used to estimate capital stock, particularly: (1) GFCF or investment ( I ) – the annual addition to the capital
Komplikasi awal setelah fraktur adalah syok yang berakibat fatal dalam beberapa jam setelah cedera, emboli lemak, yang dapat terjadi dalam 48 jam atau lebih, dan sindrom
Dalam kasus ini decision boundary yang terbentuk adalah hyperquadratics (hyperplanes, pasangan hyperplanes, hyperspheres, hyperellipsoids, hyperparaboloids,
PEMBANGUNAN GEDUNG KANTOR DINAS KELAUTAN DAN PERIKANAN KABUPATEN SUMENEP. TAHUN
Sebuah studi tahun 2007 pada pria yang berusia lebih dari 40 tahun menghubungkan konsumsi kopi jangka panjang dengan rendahnya risiko encok, kondisi peradangan yang disebabkan
Pada percobaan ini hasil yang ditampilkan berupa grafik, walaupun tidak dituliskan plot pada listing program, karena disini yang berperan untuk menampilkan
Karakteristik nilai disiplin, yaitu: pengertian terhadap perintah yang diberikan dan sudah melaksanakan perintah sesuai aturan yang ada untuk