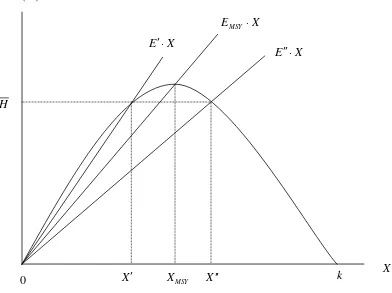
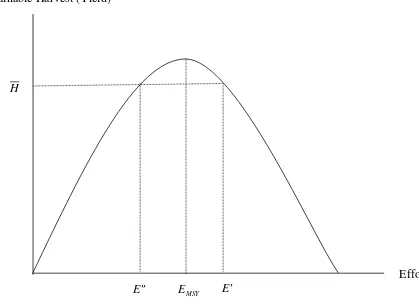
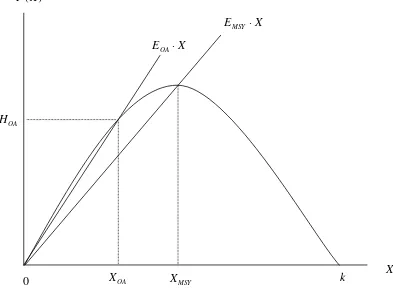
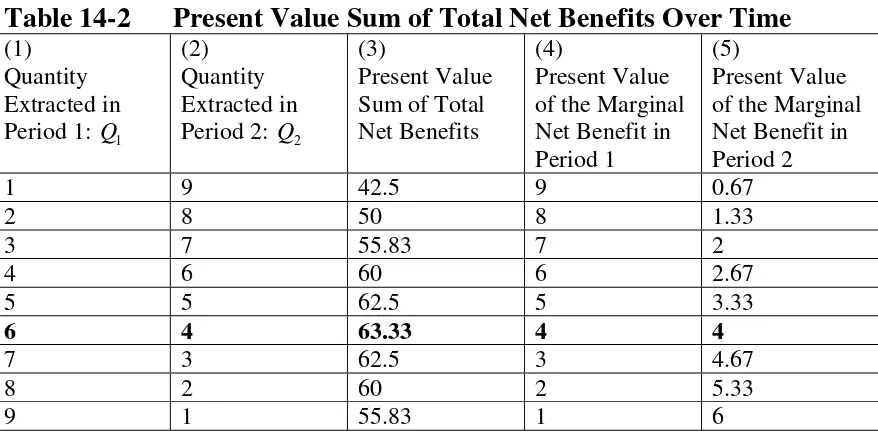
14.1 The Intertemporal Nature of Natural Resource Allocations 14.2 Present Values and Dynamic Efficiency 14.3 Nonrenewable Resource Extraction - Chapter14 Natural Resource Economics
Teks penuh
Gambar

Dokumen terkait
Sulam/bordir adalah suatu teknik yang digunakan untuk membuat hiasan- hiasan pada permukaan kain dengan mempergunakan benang hias sulam, sedangkan untuk proses pengerjaannya
Sumber : Data diolah penulis (2013) Hosmer and Lemeshow Test Step Chi-square df
Hasil uji hipotesis menunjukkan bahwa hipotesis yang diajukan dalam penelitian ini dapat diterima, yaitu ada hubungan yang signifikan antara locus of control internal dan konsep
Probabilita signifi kansi jauh lebih kecil dari 0,05, maka model dapat digunakan untuk memprediksi variabel kinerja perbankan syariah, atau dapat dikatakan bahwa variabel
Existing Surveillance and Response Capacity Several global disease surveillance systems and networks have been established to detect human outbreaks of emerging zoonotic diseases
Kode Etika Peneliti adalah acuan moral yang berlaku secara nasional bagi peneliti di unit penelitian dan pengembangan (litbang) dalam melaksanakan penelitian dan
Masing-masing antibodi memiliki daerah variabel ( variable region ) yang dapat mengenali antigen khusus dan daerah konstan ( constant region ) yang mengontrol bagaimana
[r]